
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,动点M从点A出发,以每秒1个单位长度的速度沿AB向点B匀速运动;同时,动点N从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动,过线段MN的中点G作边AB的垂线,垂足为点G,交△ABC的另一边于点P,连接PM,PN,当点N运动到点A时,M,N两点同时停止运动,设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,动点M从点A出发,以每秒1个单位长度的速度沿AB向点B匀速运动;同时,动点N从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动,过线段MN的中点G作边AB的垂线,垂足为点G,交△ABC的另一边于点P,连接PM,PN,当点N运动到点A时,M,N两点同时停止运动,设运动时间为t秒.分析 (1)根据勾股定理可得AB=10,若动点M、N相遇,则有t+3t=10,即可求出t的值;
(2)由于“点P在BC上”与“点P在点AC上”及“点M在点N的左边”与“点M在点N的右边”对应的MN、PG的表达式不同,S与t之间的函数关系式也就不同,因此需分情况讨论.只需先考虑临界位置(点P与点C重合,点M与点N重合、点N与点A重合)所对应的t的值,然后分三种情况(①0≤t≤1.4,②1.4<t<2.5,③2.5<t≤$\frac{10}{3}$)讨论,用t的代数式表示出MN和PG,就可解决问题;
(3)过点K作KD⊥AC于D,过点M作ME⊥AC于E,由于AC已知,要求△KAC的面积的最值,只需用t的代数式表示出DK,然后利用一次函数的增减性就可解决问题.
解答 解:(1)∵∠ACB=90°,AC=6,BC=8,∴AB=10,
∴t+3t=10,解得t=2.5(s),
即当t=2.5秒时,动点M,N相遇;
故答案为2.5;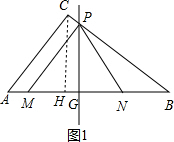
(2)过点C作CH⊥AB于H,
由S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CH得,CH=$\frac{AC•BC}{AB}$=4.8,
∴AH=$\sqrt{A{C}^{2}-C{H}^{2}}$=3.6,BH=10-3.6=6.4.
∵当点N运动到点A时,M,N两点同时停止运动,∴0≤t≤$\frac{10}{3}$.
当0≤t<2.5时,点M在点N的左边,如图1、图2,
MN=AB-AM-BN=10-t-3t=10-4t.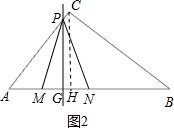
∵点G是MN的中点,∴MG=$\frac{1}{2}$MN=5-2t,
∴AG=AM+MG=t+5-2t=5-t,
∴BG=10-(5-t)=t+5.
当点P与点C重合时,点G与点H重合,
则有5-t=3.6,解得t=1.4.
当2.5<t≤$\frac{10}{3}$时,点M在点N右边,如图3,
∵MN=AM-AN=AM-(AB-BN)=t-(10-3t)=4t-10,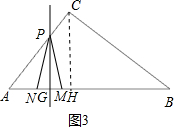
∴NG=$\frac{1}{2}$MN=2t-5,
∴AG=AN+NG=10-3t+2t-5=5-t.
综上所述:①当0≤t≤1.4时,点M在点N的左边,点P在BC上,如图1,
此时MN=10-4t,BG=t+5,PG=BG•tanB=$\frac{6}{8}$(t+5)=$\frac{3}{4}$t+$\frac{15}{4}$,
∴S=$\frac{1}{2}$MN•PG=$\frac{1}{2}$(10-4t)•($\frac{3}{4}$t+$\frac{15}{4}$)=-$\frac{3}{2}$t2-$\frac{15}{4}$t+$\frac{75}{4}$;
②当1.4<t<2.5时,点M在点N的左边,点P在AC上,如图2,
此时MN=10-4t,AG=5-t,PG=AG•tanA=$\frac{8}{6}$(5-t)=$\frac{20}{3}$-$\frac{4}{3}$t,
∴S=$\frac{1}{2}$MN•PG=$\frac{1}{2}$(10-4t)•($\frac{20}{3}$-$\frac{4}{3}$t)=$\frac{8}{3}$t2-20t+$\frac{100}{3}$;
③当2.5<t≤$\frac{10}{3}$时,点M在点N的右边,点P在AC上,如图3,
此时MN=4t-10,AG=5-t,PG=AG•tanA=$\frac{8}{6}$(5-t)=$\frac{20}{3}$-$\frac{4}{3}$t,
∴S=$\frac{1}{2}$MN•PG=$\frac{1}{2}$(4t-10)•($\frac{20}{3}$-$\frac{4}{3}$t)=-$\frac{8}{3}$t2+20t-$\frac{100}{3}$;
∴S与t之间的函数关系式为S=$\left\{\begin{array}{l}{-\frac{3}{2}{t}^{2}-\frac{15}{4}t+\frac{75}{4},0≤t≤1.4}\\{\frac{8}{3}{t}^{2}-20t+\frac{100}{3},1.4<t<2.5}\\{-\frac{8}{3}{t}^{2}+20t-\frac{100}{3},2.5<t≤\frac{10}{3}}\end{array}$;
(3)在整个运动过程中,△KAC的面积变化,最大值为4,最小值为$\frac{42}{25}$.
提示:过点K作KD⊥AC于D,过点M作ME⊥AC于E.
①当0≤t≤1.4时,点P在BC上,如图4,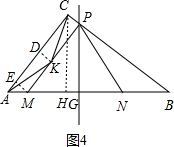
此时AM=t,BG=t+5,
∴EM=AM•sin∠EAM=$\frac{8}{10}$t=$\frac{4}{5}$t,BP=$\frac{BG}{cosB}$=$\frac{t+5}{\frac{8}{10}}$=$\frac{5}{4}$t+$\frac{25}{4}$,
∴CP=CB-BP=8-($\frac{5}{4}$t+$\frac{25}{4}$)=-$\frac{5}{4}$t+$\frac{7}{4}$.
∵EM⊥AC,KD⊥AC,PC⊥AC,
∴EM∥DK∥CP.
∵K为PM的中点,∴D为EC中点,
∴DK=$\frac{1}{2}$(CP+EM)=$\frac{1}{2}$(-$\frac{5}{4}$t+$\frac{7}{4}$+$\frac{4}{5}$t)=-$\frac{9}{40}$t+$\frac{7}{8}$,
∴S△KAC=$\frac{1}{2}$AC•DK=$\frac{1}{2}$×6×(-$\frac{9}{40}$t+$\frac{7}{8}$)=-$\frac{27}{40}$t+$\frac{21}{8}$,
∵-$\frac{27}{40}$<0,∴S△KAC随着t的增大而减小,
∴当t=0时,S△KAC取到最大值,最大值为$\frac{21}{8}$,
当t=1.4时,S△KAC取到最小值,最小值为$\frac{42}{25}$;
②当1.4<t≤$\frac{10}{3}$时,点P在AC上,如图5、图6,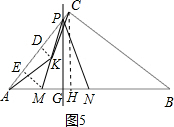
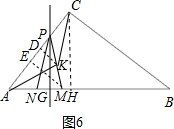
同理可得:DK为△PEM的中位线,EM=$\frac{4}{5}$t,
∴DK=$\frac{1}{2}$EM=$\frac{2}{5}$t,
∴S△KAC=$\frac{1}{2}$AC•DK=$\frac{1}{2}$×6×$\frac{2}{5}$t=$\frac{6}{5}$t.
∵$\frac{6}{5}$>0,∴S△KAC随着t的增大而增大,
∴当t=1.4时,S△KAC取到最小值,最小值为$\frac{42}{25}$;
当t=$\frac{10}{3}$时,S△KAC取到最大值,最大值为$\frac{6}{5}$×$\frac{10}{3}$=4
综上所述:△KAC的面积的最大值为4,最小值为$\frac{42}{25}$.
点评 本题主要考查了平行线分线段成比例、三角函数的定义、勾股定理、梯形中位线定理、三角形中位线定理、一次函数的增减性等知识,在解决问题的过程中,用到了分类讨论、等积法、临界值法等重要的数学思想方法,找准临界点是解决本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | A1(-2,-1),B1(2,1),C1(1,-4) | B. | A1(-1,1),B1(3,3),C1(2,-2) | ||
| C. | A1(0,0),B1(4,2),C1(3,-3) | D. | A1(-1,2),B1(3,4),C1(2,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
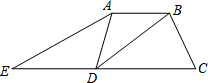 如图,在四边形ABCD中,DB平分∠ADC,∠ABC=120°,∠C=60°,∠BDC=30°;延长CD到点E,连接AE,使得∠C=2∠E.
如图,在四边形ABCD中,DB平分∠ADC,∠ABC=120°,∠C=60°,∠BDC=30°;延长CD到点E,连接AE,使得∠C=2∠E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com