
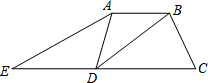
 如图,在四边形ABCD中,DB平分∠ADC,∠ABC=120°,∠C=60°,∠BDC=30°;延长CD到点E,连接AE,使得∠C=2∠E.
如图,在四边形ABCD中,DB平分∠ADC,∠ABC=120°,∠C=60°,∠BDC=30°;延长CD到点E,连接AE,使得∠C=2∠E.分析 (1)求出∠E=∠BDC,根据平行线的判定推出AB∥DC,AE∥BD,根据平行线的判定得出即可;
(2)过A作AQ⊥DC于Q,过B作BF⊥DC于F,求出四边形AQFB是平行四边形,推出AQ=BF,解直角三角形求出BC=6,BD=6$\sqrt{3}$,由三角形的面积公式得出S△DBC=$\frac{1}{2}$DB×BC=$\frac{1}{2}$DC×BF,求出BF,求出AQ,解直角三角形求出AD即可.
解答 (1)证明:∵∠C=60°,∠C=2∠E,
∴∠E=30°,
∵∠BDC=30°,
∴∠E=∠BDC,
∴AE∥BD,
∵∠ABC=120°,∠C=60°,
∴∠ABC+∠C=180°,
∴AB∥ED,
∴四边形ABDE是平行四边形;
(2)解: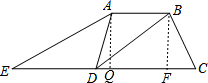
过A作AQ⊥DC于Q,过B作BF⊥DC于F,
则AQ∥BF,
∵AB∥DC,
∴四边形AQFB是平行四边形,
∴AQ=BF,
∵∠BDC=30°,∠C=60°,
∴∠DBC=90°,
∵DC=12,
∴BC=6,BD=6$\sqrt{3}$,
∵由三角形的面积公式得:S△DBC=$\frac{1}{2}$DB×BC=$\frac{1}{2}$DC×BF,
∴BF=3$\sqrt{3}$,
∴AQ=3$\sqrt{3}$,
∵DB平分∠ADC,∠BDC=30°,
∴∠ADQ=2∠BDC=60°,
∵在Rt△AQD中,∠AQD=90°,∠ADQ=60°,AQ=3$\sqrt{3}$,
∴AD=$\frac{AQ}{sin60°}$=6.
点评 本题考查了平行四边形的判定和性质,三角形内角和定理,解直角三角形的应用,能综合运用性质进行推理是解此题的关键,综合性比较强,难度适中.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,动点M从点A出发,以每秒1个单位长度的速度沿AB向点B匀速运动;同时,动点N从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动,过线段MN的中点G作边AB的垂线,垂足为点G,交△ABC的另一边于点P,连接PM,PN,当点N运动到点A时,M,N两点同时停止运动,设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,动点M从点A出发,以每秒1个单位长度的速度沿AB向点B匀速运动;同时,动点N从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动,过线段MN的中点G作边AB的垂线,垂足为点G,交△ABC的另一边于点P,连接PM,PN,当点N运动到点A时,M,N两点同时停止运动,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
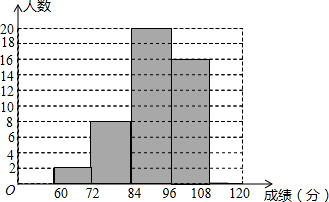 朝宗实验学校初三年级的同学参加了吉州市的模拟统考,该校数学教师对本班数学成绩(成绩取整数,满分为120分)作了统计分析,绘制成频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题.
朝宗实验学校初三年级的同学参加了吉州市的模拟统考,该校数学教师对本班数学成绩(成绩取整数,满分为120分)作了统计分析,绘制成频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题. | 频数 | 频率 | |
| 60<x≤72 | 2 | 0.04 |
| 72<x≤84 | 8 | 0.16 |
| 84<x≤96 | 20 | a |
| 96<x≤108 | 16 | 0.32 |
| 108<x≤120 | b | 0.08 |
| 合计 | 50 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com