
分析 (1)首先根据条件确定|a-b|≥1,|b-c|≥1,|a-c|≥0,再由|a-b|+|c-a|=1可得c=a,|a-b|=1,进而可得答案;
(2)此题要分两种情况:①a在b的左侧,相隔1个单位;②a在b的右侧,相隔1个单位,再根据速度×时间=路程可列出方程;
(3)此题要分4种情况:①当a=-3,b=-2时,D在AB之间;D在B的右侧;②当a=-3,b=-4时,D在AB之间;D在B的左侧.
解答 解:(1)∵a、b、c为整数,a≠b,
∴|a-b|≥1,|b-c|≥1,|a-c|≥0,
∵|a-b|+|c-a|=1
∴c-a=0,|a-b|=1,
∴a=c,
∴|b-a|+|a-c|+|c-b|=1+0+1=2;
(2)如图1: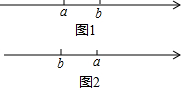 由题意得:(2+3)t-1=52,
由题意得:(2+3)t-1=52,
解得:t=$\frac{52}{5}$;
如图2:由题意得:5t+1=51,
解得:t=10;
答:经过$\frac{52}{5}$秒或10秒时间A,B相距51个单位长度;
(3) 若数轴上点A,B,D对应的数分别为a,b,d,当a=-3,且BD=$\frac{2}{3}$AD时,求点D所对应的数
若数轴上点A,B,D对应的数分别为a,b,d,当a=-3,且BD=$\frac{2}{3}$AD时,求点D所对应的数
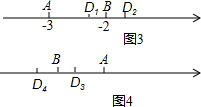
如图3,当a=-3,b=-2时,
∵BD=$\frac{2}{3}$AD,
∴D1=-2.4;D2=0;
如图4,当a=-3,b=-4时,
∵BD=$\frac{2}{3}$AD,
∴D1=-3.6;D2=-6.
点评 此题主要考查了一元一次方程的应用和数轴,关键是正确理解题意,找出题目中的等量关系,注意要分情况进行讨论,不要漏解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
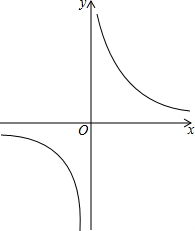 反比例函数y=$\frac{k-1}{x}$如图,则:
反比例函数y=$\frac{k-1}{x}$如图,则:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
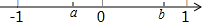 实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$的结果是-ab+b-a.
实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$的结果是-ab+b-a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2ab | B. | +2ab | C. | +4ab | D. | -4ab |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | a | C. | $\sqrt{2}$ | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com