

���� ��1�����÷Ǹ��Լ������a��b���ɵó����ۣ�
��2�����жϳ���DEF�ա�BDO���ó�EF��OF����������ı���OBEF�����Ϊ18���ٷ�����������ۼ��㼴�ɣ�
��3�����жϳ���PBO�ա�MPN�������жϳ���BAQ�ǵ���ֱ�������Σ����ɵó�OQ=4���ɵó����ۣ�
��� �⣺��1����$\sqrt{a-4}$+|4-b|=0��
��a-4=0��4-b=0��
��a=4��b=4��
��A��4��0����B��0��4����
��2���ɣ�1��֪��B��0��4����
��OB=4��
��CΪOA���е㣬
��OC=2��
��C��2��0����
�ߵ�C����y��ĶԳƵ�D��
��D��-2��0����
��OD=2��
��BDΪֱ�DZ��ڵڶ�����������Rt��BDE��
����ͼ�� ��BD=BE����DBE=90��ʱ������E��EH��OB��H��
��BD=BE����DBE=90��ʱ������E��EH��OB��H��
���BHE=90�㣬
���BEH+��HBE=90�㣬
�ߡ�DBE=90�㣬
���HBE+��OBD=90�㣬
���BEH=��OBD��
�ڡ�OBD�͡�HEB�У�$\left\{\begin{array}{l}{��BOD=��EHB=90��}\\{��OBD=��BEH}\\{BD=BE}\end{array}\right.$��
���OBD�ա�HEB��
��BH=OD��EH=OB��
��D��-2��0����B��0��4����
��OB=4��OD=2��
��BH=2��EH=4��
��OH=OB+BH=6����E��-4��6����
��EF=OH=6��OF=EH=4��
��S�ı���OBEF=$\frac{1}{2}$��OB+EF����OF=20��
��ֱ��y=kx-4k���ı���OBEF��Ϊ�����ȵ������֣�
��S�ı���OBGF=$\frac{1}{2}$S�ı���OBEF=10��
��S�ı���OBGF=$\frac{1}{2}$��FG+OB����OF=$\frac{1}{2}$����FG+4����4=2��FG+4��=10��
��FG=1����G��-4��1��
��G��-4��1������ֱ��y=kx-4k���ã�1=-4k-4k��
��k=-$\frac{1}{8}$��
����ͼ1���� DE=BD����BDE=90��ʱ��
DE=BD����BDE=90��ʱ��
���EDF+��BDO=90�㣬
��EF��x���ڵ�F��
���EDF+��DEF=90�㣬
���DEF=��BDO��
�ڡ�DEF�͡�BDO�У�$\left\{\begin{array}{l}{��DFE=��BOD=90��}\\{��DEF=��BDO}\\{DE=BD}\end{array}\right.$��
���DEF�ա�BDO��
��EF=OD=2��DF=OB=4��
��OF=6��
��F��-6��2����
��S�ı���OBEF=$\frac{1}{2}$��EF+OB��•OF=$\frac{1}{2}$����2+4����6=18��
��ֱ��y=kx-4k���ı���OBEF��Ϊ�����ȵ������֣�
��ֱ��y=kx-4k�ֳɵ������ֵ����Ϊ9��
��ֱ��y=kx-4k���A��4��0����
���ֱ��y=kx-4k���߶�EF�ཻ��
��S�ı���OHGF=9��
��H��0��-4k����
��OH=-4k��
��G��ĺ�����Ϊ-6��
��G��-6��-10k����
��FG=-10k��
��S�ı���OHGF=$\frac{1}{2}$��-4k-10k����6=9��
��k=-$\frac{3}{14}$��
��ֱ��y=kx-4k�ٺ��߶�EB�ཻ��
��S��MBN=9��
��N��0��-4k����
��BN=4��k+1����
��B��0��4����E��-6��2����
��ֱ��BE�Ľ���ʽΪy=$\frac{1}{3}$x+4�ڣ�
�����٢ڵã���M�ĺ�����Ϊ$\frac{12��k+1��}{3k-1}$��
��S��MBN=$\frac{1}{2}$��4��k+1����$\frac{12��k+1��}{1-3k}$=9��
��k=$\frac{-25-5\sqrt{15}}{16}$���ᣩ��k=$\frac{-25+5\sqrt{15}}{16}$��
��������������k��ֵΪ-$\frac{1}{8}$��-$\frac{3}{14}$��$\frac{-25+5\sqrt{15}}{16}$��
��3����ͼ2��
��M��MN��x�ᣬ����ΪN��
�ߡ�BPM=90�㣬
���BPO+MPN=90�㣮
�ߡ�AOB=��MNP=90�㣬
���BPO=��PMN����PBO=��MPN��
��BP=MP��
���PBO�ա�MPN��
��MN=OP��PN=AO=BO��
��OP=OA+AP=PN+AP=AN��
��MN=AN����MAN=45�㣮
�ߡ�BAO=45�㣬
���BAQ�ǵ���ֱ�������Σ�
��OB=OQ=4��
������P����ô����OQ�ij����䣮
���� ������һ�κ����ۺ��⣬��Ҫ�����˷Ǹ��ԣ�ȫ�������ε��ж������ʣ����ε������ʽ�������ε������ʽ������ֱ�������ε��ж������ʣ��Ȿ��Ĺؼ������k��ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ֧��20Ԫ | B�� | ����20Ԫ | C�� | ֧��80Ԫ | D�� | ����80Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����֪��ABC�У���C=90�㣬AB=5cm��AC=3cm��BC=4cm��AD�ǡ�CAB��ƽ���ߣ���BC����D��DE��AB��E����
��ͼ��ʾ����֪��ABC�У���C=90�㣬AB=5cm��AC=3cm��BC=4cm��AD�ǡ�CAB��ƽ���ߣ���BC����D��DE��AB��E�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��COB=2��AOC��ODƽ�֡�AOB����AOC=20�㣬���COD�Ķ�����
��ͼ����֪��COB=2��AOC��ODƽ�֡�AOB����AOC=20�㣬���COD�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
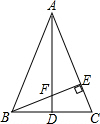 ��ͼ����ABC�У�AB=AC��BE��AC�ڵ�E��AD��BC�ڵ�D����ABE=45�㣬AD��BE���ڵ�F������CF��
��ͼ����ABC�У�AB=AC��BE��AC�ڵ�E��AD��BC�ڵ�D����ABE=45�㣬AD��BE���ڵ�F������CF���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com