
【题目】如图1,正方形ABCD和正方形AEFG,连接DG,BE.
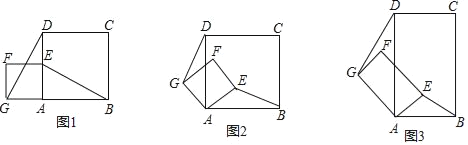
(1)发现:当正方形AEFG绕点A旋转,如图2,①线段DG与BE之间的数量关系是 ;②直线DG与直线BE之间的位置关系是 .
(2)探究:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,证明:直线DG⊥BE.
(3)应用:在(2)情况下,连结GE(点E在AB上方),若GE∥AB,且AB=![]() ,AE=1,则线段DG是多少?(直接写出结论)
,AE=1,则线段DG是多少?(直接写出结论)
【答案】(1)BE=DG,BE⊥DG;(2)证明见解析;(3)![]()
【解析】
(1)先判断出△ABE≌△ADG,进而得出BE=DG,∠ABE=∠ADG,再利用等角的余角相等即可得出结论;
(2)先利用两边对应成比例夹角相等判断出△ABE∽△ADG,得出∠ABE=∠ADG,再利用等角的余角相等即可得出结论;
(3)先求出BE,进而得出BE=AB,即可得出四边形ABEG是平行四边形,进而得出∠AEB=90°,求出BE,借助(2)得出的相似,即可得出结论.
(1)①∵四边形ABCD和四边形AEFG是正方形,
∴AE=AG,AB=AD,∠BAD=∠EAG=90°,
∴∠BAE=∠DAG,
在△ABE和△ADG中,
 ,
,
∴△ABE≌△ADG(SAS),
∴BE=DG;
②如图2,延长BE交AD于G,交DG于H,

由①知,△ABE≌△ADG,
∴∠ABE=∠ADG,
∵∠AGB+∠ABE=90°,
∴∠AGB+∠ADG=90°,
∵∠AGB=∠DGH,
∴∠DGH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG
(2)∵四边形ABCD与四边形AEFG都为矩形,
∴∠BAD=∠DAG,
∴∠BAE=∠DAG,
∵AD=2AB,AG=2AE,
∴![]() ,
,
∴△ABE∽△ADG,
∴∠ABE=∠ADG,
∵∠AGB+∠ABE=90°,
∴∠AGB+∠ADG=90°,
∵∠AGB=∠DGH,
∴∠DGH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG;
(3)如图4,(为了说明点B,E,F在同一条线上,特意画的图形)

∵EG∥AB,
∴∠DME=∠DAB=90°,
在Rt△AEG中,AE=1,
∴AG=2AE=2,
根据勾股定理得,EG=![]() ,
,
∵AB=![]() ,
,
∴EG=AB,
∵EG∥AB,
∴四边形ABEG是平行四边形,
∴AG∥BE,
∵AG∥EF,
∴点B,E,F在同一条直线上如图5,

∴∠AEB=90°,
在Rt△ABE中,根据勾股定理得,BE=![]() =2,
=2,
由(3)知,△ABE∽△ADG,
∴![]() ,
,
∴![]() ,
,
∴DG=4.


科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字:﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树状图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在直线y=﹣x上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22时,
教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45时,教学楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).
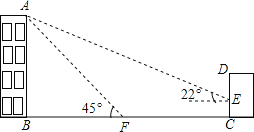
(1)求教学楼AB的高度;
(2)学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22≈![]() ,cos22≈
,cos22≈![]() ,tan22≈
,tan22≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
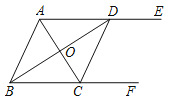
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADB=30°,BD=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
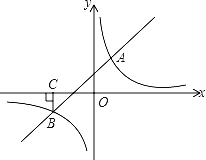
(1)求反比例函数的解析式;
(2)过B点作BC⊥x轴,垂足为C,若P是反比例函数图象上的一点,连接PC,PB,求当△PCB的面积等于5时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中, 每个小正方形的边长是1个单位长度)
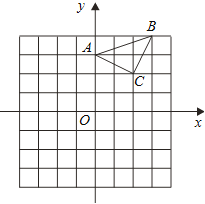
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2︰1,并直接写出C2点的坐标及△A2BC2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c中,b=4a,它的图象如图,有以下结论:①c>0;②a+b+c>0;③a﹣b+c>0 ④b2﹣4ac<0;⑤abc<0;⑥4a>c;其中正确的为_____(填序号).
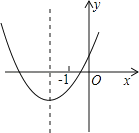
查看答案和解析>>
科目:初中数学 来源: 题型:
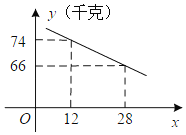
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示.
(1)求y与x之间的函数关系式.
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实7000千克.
(3)当增种果树多少棵时,果园的总产量w(千克)最大?此时每棵果树的产量是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com