
【题目】如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则△ABC的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】将△BPC绕点B逆时针旋转60°得△BEA,根据旋转的性质得BE=BP=4,AE=PC=5,∠PBE=60°,则△BPE为等边三角形,得到PE=PB=4,∠BPE=60°,在△AEP中,AE=5,延长BP,作AF⊥BP于点F.AP=3,PE=4,根据勾股定理的逆定理可得到△APE为直角三角形,且∠APE=90°,即可得到∠APB的度数,在直角△APF中利用三角函数求得AF和PF的长,则在直角△ABF中利用勾股定理求得AB的长,进而求得三角形ABC的面积.
∵△ABC为等边三角形,
∴BA=BC,
可将△BPC绕点B逆时针旋转60°得△BEA,连EP,且延长BP,作AF⊥BP于点F.如图,
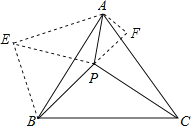
∴BE=BP=4,AE=PC=5,∠PBE=60°,
∴△BPE为等边三角形,
∴PE=PB=4,∠BPE=60°,
在△AEP中,AE=5,AP=3,PE=4,
∴AE2=PE2+PA2,
∴△APE为直角三角形,且∠APE=90°,
∴∠APB=90°+60°=150°.
∴∠APF=30°,
∴在直角△APF中,AF=![]() AP=
AP=![]() ,PF=
,PF=![]() AP=
AP=![]() .
.
∴在直角△ABF中,AB2=BF2+AF2=(4+![]() )2+(
)2+(![]() )2=25+12
)2=25+12![]() .
.
则△ABC的面积是![]() AB2=
AB2=![]() (25+12
(25+12![]() )=9+
)=9+![]() .
.
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,sin∠BAC= ![]() ,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G,则AG的长为 .
,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G,则AG的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(4,1),B(5,4),将线段AB绕点A逆时针旋转90°得线段AC,则点C的坐标为( )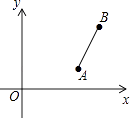
A.(1,2)
B.(2,1)
C.(7,0)
D.(1,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
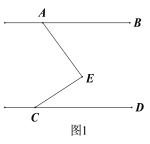
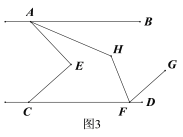
【题目】如图,已知AB∥CD,点E在直线AB,CD之间.
(1)求证:∠AEC=∠BAE+∠ECD;
(2)若AH平分∠BAE,将线段CE沿射线CD平移至FG.
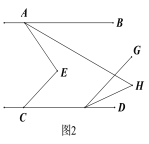
①如图2,若∠AEC=90°,FH平分∠DFG,求∠AHF的度数;
②如图3,若FH平分∠CFG,试判断∠AHF与∠AEC的数量关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,且AB=2cm,点P为弧AB上一动点(不与A,B重合), ![]() =
= ![]() ,过点D作⊙O的切线交PB的延长线于点C.
,过点D作⊙O的切线交PB的延长线于点C. 
(1)试证明AB∥CD;
(2)填空: ①当BP=1cm时,PD=cm;
②当BP=cm时,四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
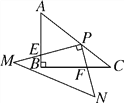
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4.Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了丰富学生的大课间活动,准备购进一批跳绳,已知2根短绳和1根长绳共需56元,1根短绳和2根长绳共需82元.
(1)求每根短绳和每根长绳的售价各是多少元?
(2)学校准备购进这两种跳绳共50根,并且短绳的数量不超过长绳数量的2倍,总费用不超过1020元,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com