
【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
【答案】
(1)解:设该运动员共出手x个3分球,根据题意,得
![]() =12,
=12,
解得x=640,
0.25x=0.25×640=160(个),
答:运动员去年的比赛中共投中160个3分球
(2)解:小亮的说法不正确;
3分球的命中率为0.25,是40场比赛来说的平均水平,而在其中的一场比赛中,命中率并不一定是0.25,所以该运动员这场比赛中不一定投中了5个3分球
【解析】(1)设该运动员共出手x个3分球,用没有命中的概率与共出手次数的乘积比上篮球运动员去年共参加篮球比赛的场次等于平均每场未未投中的次数列出方程,求解即可;(2)小亮的说法不正确;这是一道用样本来估计总体的题,3分球的命中率为0.25,是40场比赛来说的平均水平,而在其中的一场比赛中,命中率并不一定是0.25,所以该运动员这场比赛中不一定投中了5个3分球。
【考点精析】解答此题的关键在于理解概率的意义的相关知识,掌握任何事件的概率是0~1之间的一个确定的数,它度量该事情发生的可能性.小概率事件很少发生,而大概率事件则经常发生.知道随机事件的概率有利于我们作出正确的决策.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】常德市为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.若王大爷家一月份用水16吨,需交水费49元,二月份用水20吨,需交水费63元.
(1)求每吨水的基础价和调节价;
(2)若王大爷家三月份交了77元的水费,请问他家用了多少吨水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三角板(含30°、60°角)和一把直尺摆放位置如图所示,直尺与三角板的一角相交于点A,一边与三角板的两条直角边分别相交于点D、点E,且CD=CE,点F在直尺的另一边上,那么∠BAF的大小为°.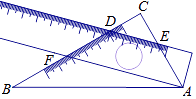
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
最喜爱的传统文化项目类型频数分布表
项目类型 | 频数 | 频率 |
书法类 | 18 | a |
围棋类 | 14 | 0.28 |
喜剧类 | 8 | 0.16 |
国画类 | b | 0.20 |
根据以上信息完成下列问题: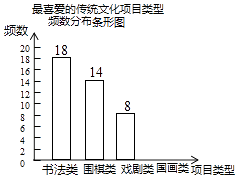
(1)直接写出频数分布表中a的值;
(2)补全频数分布条形图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行阶梯式计量水价.每户每月用水量不超过25吨,收
费标准为每吨a元;若每户每月用水量超过25吨时,其中前25吨还是每吨a元,超出的部
分收费标准为每吨b元.下表是小明家一至四月份用水量和缴纳水费情况.根据表格提供的数
据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 16 | 18 | 30 | 35 |
水费(元) | 32 | 36 | 65 | 80 |
(1)a=________;b=________;
(2)若小明家五月份用水32吨,则应缴水费 元;
(3)若小明家六月份应缴水费102.5元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店去年3至8月销售吐鲁番葡萄、哈密瓜的情况如下表:
3月 | 4月 | 5月 | 6月 | 7月 | 8月 | |
吐鲁番葡萄(单位:百公斤) | 4 | 8 | 5 | 8 | 10 | 13 |
哈密瓜(单位:百公斤) | 8 | 7 | 9 | 7 | 10 | 7 |
(1)请你根据以上数据填写下表:
平均数/百公斤 | 方差 | |
吐鲁番葡萄 | 8 | 9 |
哈密瓜 |
(2)请你根据上述信息,对这两种水果在去年3月份至8月份的销售情况进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
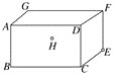
【题目】长方体敞口玻璃罐,长、宽、高分别为16 cm、6 cm和6 cm,在罐内点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外壁,在长方形ABCD中心的正上方2 cm处,则蚂蚁到达饼干的最短距离是多少cm.( )
A. 7![]() B.
B. ![]()
C. 24D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com