练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AD是⊙O的弦，AB经过圆心O，交⊙O于点C．∠DAB=∠B=30°．

    （1）直线BD是否与⊙O相切？为什么？

    （2）连接CD，若CD=5，求AB的长．

    【答案】解：（1）直线BD与⊙O相切．

    如图

    连接OD，CD，

    ∵∠DAB=∠B=30°，∴∠ADB=120°，

    ∵OA=OD，∴∠ODA=∠OAD=30°，

    ∴∠ODB=∠ADB﹣∠ODA=120°﹣30°=90°．

    所以直线BD与⊙O相切．

    （2）连接CD，

    ∠COD=∠OAD+∠ODA=30°+30°=60°，

    又OC=OD

    ∴△OCD是等边三角形，

    即：OC=OD=CD=5=OA，

    ∵∠ODB=90°，∠B=30°，

    ∴OB=10，

    ∴AB=AO+OB=5+10=15．

    【解析】略

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，△ABE和△CDF为直角三角形，∠AEB＝∠CFD＝90°，AE＝CF＝5，BE＝DF＝12，则EF的长是( )

    A. 7 B. 8 C. 7 D. 7

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：△ABC是边长为3的等边三角形,以BC为底边作一个顶角为120等腰△BDC.点M、点N分别是AB边与AC边上的点,并且满足∠MDN=60

    （1）如图1，当点D在△ABC外部时，求证：BM+CN=MN；

    （2）当点D在△ABC内部时，其它条件不变，请在图2中补全图形，并直接写出△AMN的周长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

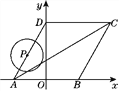
    【题目】如图，菱形ABCD的顶点A，B在x轴上，点A在点B的左侧，点D在y轴的正半轴上，∠BAD＝60°，点A的坐标为(－2，0)．

    (1)求线段AD所在直线的表达式；

    (2)动点P从点A出发，以每秒1个单位长度的速度，按照A→D→C→B→A的顺序在菱形的边上匀速运动一周，设运动时间为t秒．求t为何值时，以点P为圆心、以1为半径的圆与对角线AC相切？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的切线，B为切点，圆心在AC上，∠A=30°，D为 的中点．

    （1）求证：AB=BC；

    （2）求证：四边形BOCD是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是一副秋千架，左图是从正面看，当秋千绳子自然下垂时，踏板离地面0.5m（踏板厚度忽略不计）， 右图是从侧面看，当秋千踏板荡起至点B位置时，点B离地面垂直高度BC为1m，离秋千支柱AD的水平距离BE为1.5m（不考虑支柱的直径）.求秋千支柱AD的高.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数.将骰子抛掷两次，掷第一次，将朝上一面的点数记为，掷第二次，将朝上一面的点数记为，则点（）落在直线上的概率为：

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司生产的一种健身产品在市场上受到普遍欢迎，每年可在国内、国外市场上全部售完，该公司的年产量为6千件，若在国内市场销售，平均每件产品的利润（元）与国内销售数量（千件）的关系为：若在国外销售，平均每件产品的利润（元）与国外的销售数量t（千件）的关系为：

    （1）用的代数式表示t为：t= ；当0＜≤4时，与的函数关系式为：= ；当4≤＜ 时，=100；

    （2）求每年该公司销售这种健身产品的总利润W（千元）与国内的销售数量ｘ（千件）的函数关系式，并指出ｘ的取值范围；

    （3）该公司每年国内、国外的销量各为多少时，可使公司每年的总利润最大？最大值为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知点A（0，2），△AOB为等边三角形，P是x轴上一个动点（不与原O重合），以线段AP为一边在其右侧作等边三角形△APQ．

    （1）求点B的坐标；

    （2）在点P的运动过程中，∠ABQ的大小是否发生改变？如不改变，求出其大小；如改变，请说明理由．

    （3）连接OQ，当OQ∥AB时，求P点的坐标．

    查看答案和解析>>

    同步练习册答案