
【题目】已知:△ABC是边长为3的等边三角形,以BC为底边作一个顶角为120![]() 等腰△BDC.点M、点N分别是AB边与AC边上的点,并且满足∠MDN=60
等腰△BDC.点M、点N分别是AB边与AC边上的点,并且满足∠MDN=60![]()
(1)如图1,当点D在△ABC外部时,求证:BM+CN=MN;
(2)当点D在△ABC内部时,其它条件不变,请在图2中补全图形,并直接写出△AMN的周长.

【答案】(1)证明见解析;(2)3.
【解析】
(1)延长AB至F,使BF=CN,连接DF,证明△BDF≌△CDN,△DMN≌△DMF即可得到结论;
(2)延长BD交AC于P,延长CD交AB于Q,截取KP=QM,连接DK.通过证明△BDQ≌△CDP,△MDQ≌△KDP,△MDN≌△KDN可得△AMN的周长=AQ+AP=3.
(1)延长AB至F,使BF=CN,连接DF.
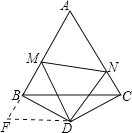
∵△BDC是等腰三角形,且∠BDC=120°,∴∠BCD=∠DBC=30°.
∵△ABC是边长为3的等边三角形,∴∠ABC=∠BAC=∠BCA=60°,∴∠DBA=∠DCA=90°,∴∠DBF=∠DBA=∠DCA=90°.
在△BDF和△CND中,∵BF=CN,∠DBF=∠DCN,DB=DC,∴△BDF≌△CDN,∴∠BDF=∠CDN,DF=DN.
∵∠MDN=60°,∴∠BDM+∠CDN=60°,∴∠BDM+∠BDF=60°,∠FDM=60°=∠MDN,DM为公共边,∴△DMN≌△DMF,∴MN=MF.
∵MF=BM+BF=MB+CN,∴MN=BM+CN.
(2)延长BD交AC于P,延长CD交AB于Q,截取KP=QM,连接DK.
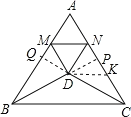
∵△BDC是等腰三角形,且∠BDC=120°,∴BD=CD,∠DBC=∠DCB=30°,∠BDQ=∠CDP=60°.
又∵△ABC等边三角形,∴∠ABC=∠ACB=60°,∴∠MBD=∠PCD=30°,CQ⊥AB,BP⊥AC,∴AQ=BQ![]() AB
AB![]() ,AP=PC
,AP=PC![]() AC
AC![]() .
.
在△BDQ和△CDP中,∵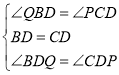 ,∴△BDQ≌△CDP(ASA),∴BQ=PC,QD=PD.
,∴△BDQ≌△CDP(ASA),∴BQ=PC,QD=PD.
∵CQ⊥AB,BP⊥AC,∴∠MQD=∠DPK=90°.
在△MDQ与△KDP中,
∵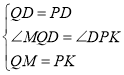 ,
,
∴△MDQ≌△KDP(SAS),
∴∠QDM=∠PDK,DM=DK.
∵∠BDQ=60°,∠MDN=60°,∴∠QDM+∠PDN=60°,
∴∠PDK+∠PDN=60°,即∠KDN=60°.
在△MDN与△KDN中,∵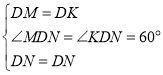 ,∴△MDN≌△KDN(SAS),
,∴△MDN≌△KDN(SAS),
∴MN=KN=NP+PK,
∴△AMN的周长=AM+AN+MN=AM+AN+NP+PK=AM+AN+NP+QM=AQ+AP![]() 3.
3.
故△AMN的周长为3.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
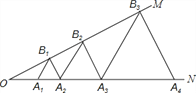
【题目】如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2017= ______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本的作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法.
我们有多少种剪法,图1是其中的一种方法:

定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行以“助人为乐,乐在其中”为主题的演讲比赛,比赛设一个第一名,一个第二名,两个并列第三名.前四名中七、八年级各有一名同学,九年级有两名同学,小蒙同学认为前两名是九年级同学的概率是![]() ,你赞成他的观点吗?请用列表法或画树形图法分析说明.
,你赞成他的观点吗?请用列表法或画树形图法分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN,与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )

A. r B. ![]() r C. 2r D.
r C. 2r D. ![]() r
r
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C.∠DAB=∠B=30°.
(1)直线BD是否与⊙O相切?为什么?
(2)连接CD,若CD=5,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∴P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交边AD于点F,交CD的延长线于点G.

(1)求证:△APB≌△APD;
(2)已知DF:FA=1:2,设线段DP的长为x,线段PF的长为y.
①求y与x的函数关系式;
②当x=6时,求线段FG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com