
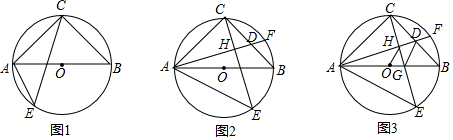
分析 (1)由圆周角定理可知∠ACB=90°,从而可证明△ABC是等腰直角三角形;
(2)由于$\widehat{CF}$=$\widehat{BE}$,所以∠CAF=∠BAE,从而可证∠BCE=∠CAF,由于∠BCE+∠ACE=90°,所以∠CAH+∠ACH=90°,从而可知CE⊥AF;
(3)过点B作BK⊥CB于点B,交CE于点K,易证△ACD≌△CBK,BK=CD,∠BKG=∠ADC,从而易证△BGK≌△BDG,所以BK=DB,所D为CB中点,过点O作NO⊥OH交AH于点N,连接CO,
易证△ANO≌△CHO,从而可知△NOH是等腰直角三角形,因为OH=$\sqrt{2}$,所以由勾股定理可知:NH=2,CH=AN=NH=2,在等腰Rt△ACB中,tan∠HAG=$\frac{1}{3}$,所以HG=$\frac{4}{3}$,DH=1,从而可求出DG=$\frac{5}{3}$
解答 解:(1)在⊙O中,∠B=∠AEC=45°,
∵AB为直径,
∴∠ACB=90°,
∴△ABC是等腰直角三角形,
(2)∵$\widehat{CF}$=$\widehat{BE}$,
∴∠CAF=∠BAE
∴∠BCE=∠BAE,
∴∠BCE=∠CAF,
∵∠BCE+∠ACE=90°,
∴∠CAH+∠ACH=90°,
∴CE⊥AF
(3)由(2)得:过点B作BK⊥CB于点B,交CE于点K,
易证△ACD≌△CBK
∴BK=CD,∠BKG=∠ADC,
∵∠ADC=∠BDG,
∴∠BKG=∠BDG,
易证△BGK≌△BDG
∴BK=DB,
∴D为CB中点,
∴tan∠CAH=tan∠DCH=$\frac{1}{2}$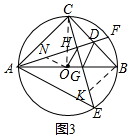
在△ACB中,过点O作NO⊥OH交AH于点N,连接CO,
易证△ANO≌△CHO,
∴CH=AN,ON=OH,
∴△NOH是等腰直角三角形,
∵tan∠CAH=$\frac{CH}{AH}$=$\frac{1}{2}$,
∴CH=$\frac{1}{2}$AH,
∴AN=NH,
∵OH=$\sqrt{2}$,
∴由勾股定理可知:NH=2,
∴CH=AN=NH=2
∴AH=4,
在等腰Rt△ACB中,
tan∠HAG=$\frac{1}{3}$,
∴HG=$\frac{4}{3}$,DH=1,
∴DG=$\frac{5}{3}$
点评 本题考查圆的综合问题,涉及全等三角形的判定与性质,锐角三角函数,解直角三角形,等腰直角三角形的判定与性质,勾股定理知识,综合程度较高,需要学生灵活运用所学知识.


科目:初中数学 来源: 题型:解答题
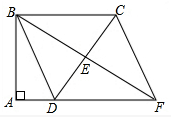 如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
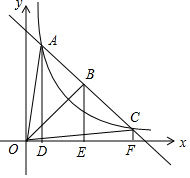 如图,直线l与函数y=$\frac{k}{x}$的图象相交,A、B、C是直线l的三点,过点A、B、C分别作x轴的垂线,垂足分别为D、E、F,连接OA、OB、OC,设△OAD的面积是S1,△OBE的面积是S2,△OCF的面积是S3,则( )
如图,直线l与函数y=$\frac{k}{x}$的图象相交,A、B、C是直线l的三点,过点A、B、C分别作x轴的垂线,垂足分别为D、E、F,连接OA、OB、OC,设△OAD的面积是S1,△OBE的面积是S2,△OCF的面积是S3,则( )| A. | S1<S2<S3 | B. | S1=S2=S3 | C. | S2>S1>S3 | D. | S3=S1<S2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
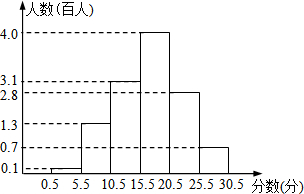 2017年3月27日是第22个全国中小学生安全教育日,某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如下“频数分布直方图”,请回答:
2017年3月27日是第22个全国中小学生安全教育日,某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如下“频数分布直方图”,请回答:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
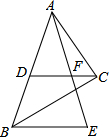 如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=$\frac{1}{3}$CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )
如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=$\frac{1}{3}$CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )| A. | 6 | B. | 4 | C. | 7 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
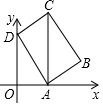 如图,在平面直角坐标系中,矩形ABCD的顶点A、D在坐标轴上,其坐标分别为(2,0),(0,4),对角线AC⊥x轴.
如图,在平面直角坐标系中,矩形ABCD的顶点A、D在坐标轴上,其坐标分别为(2,0),(0,4),对角线AC⊥x轴.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com