
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=![]() x2��
x2��![]() x��
x��![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C���Գ�����x�ύ�ڵ�D����E��4��n�����������ϣ�
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C���Գ�����x�ύ�ڵ�D����E��4��n�����������ϣ�
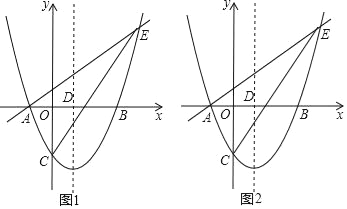
��1����ֱ��AE�Ľ���ʽ��
��2����PΪֱ��CE�·��������ϵ�һ�㣬����PC��PE������PCE��������ʱ����P�����ꣿ
��3����G���߶�CE���е㣬��������y=![]() x2��
x2��![]() x��
x��![]() ��x��������ƽ�Ƶõ���������y�䣬y��������D��y���Ķ���Ϊ��F������������y���ĶԳ����ϣ��Ƿ���ڵ�Q��ʹ����FGQΪ���������Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
��x��������ƽ�Ƶõ���������y�䣬y��������D��y���Ķ���Ϊ��F������������y���ĶԳ����ϣ��Ƿ���ڵ�Q��ʹ����FGQΪ���������Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1) y= ![]() x+
x+ ![]() (2) P��2����
(2) P��2����![]() ��(3) ��3��
��(3) ��3��![]() ����3��
����3��![]() ����3��2
����3��2![]() ����3����
����3����![]() ��
��
�������������������1�������ߵĽ���ʽ�ɱ���Ϊy=![]() (x+1)(x-3)���Ӷ��ɵõ���A�͵�B�����꣬Ȼ������õ�E�����꣬��ֱ��AE�Ľ���ʽΪy=kx+b������A�͵�E������������k��b��ֵ���Ӷ��õ�AE�Ľ���ʽ��
(x+1)(x-3)���Ӷ��ɵõ���A�͵�B�����꣬Ȼ������õ�E�����꣬��ֱ��AE�Ľ���ʽΪy=kx+b������A�͵�E������������k��b��ֵ���Ӷ��õ�AE�Ľ���ʽ��
��2����ֱ��CE�Ľ���ʽΪy=mx-![]() ������E��������뼴��ȷ��ֱ��CE�Ľ���ʽ������P��PF��y�ᣬ��CE���F�����P������Ϊ��x��
������E��������뼴��ȷ��ֱ��CE�Ľ���ʽ������P��PF��y�ᣬ��CE���F�����P������Ϊ��x��![]() x2
x2![]() x
x![]() �������PF��ֵ����ʾ����EPC������������ö��κ��������ʿ����x��ֵ���Ӷ��õ���P�����ꣻ
�������PF��ֵ����ʾ����EPC������������ö��κ��������ʿ����x��ֵ���Ӷ��õ���P�����ꣻ
��3����ƽ�ƺ�������߾�����D���ɵõ���F�����꣬�����е����깫ʽ����õ�G�����꣬Ȼ���ΪFG=FQ��GF=GQ��QG=QF���������⼴��.
�⣺��1����y=![]() x2-
x2-![]() x-
x-![]() ��
��
��y=![]() (x+1)(x-3).
(x+1)(x-3).
��A��-1��0����B��3��0��.
��x=4ʱ��y=![]() .
.
��E��4��![]() ����
����
��ֱ��AE�Ľ���ʽΪy=kx+b������A�͵�E���������ã�
 ��
��
�����k=![]() ��b=
��b=![]() ��
��
��ֱ��AE�Ľ���ʽΪy=![]() x+
x+![]()
��2����ֱ��CE�Ľ���ʽΪy=mx-![]() ������E����������4m-
������E����������4m-![]() =
=![]() �������m=
�������m=![]() .
.
��ֱ��CE�Ľ���ʽΪy=![]() x-
x-![]() .
.
����P��PF��y�ᣬ��CE���F����ͼ����ʾ.
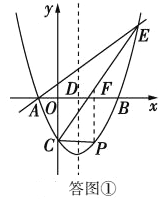
���P��������x��![]() x2
x2![]() x
x![]() �������F��x��
�������F��x��![]() x
x![]() ����
����
��FP=(![]() x
x![]() )-(
)-(![]() x2
x2![]() x
x![]() )=-
)=-![]() x2+
x2+![]() x��
x��
���EPC�����=![]() ��(-
��(-![]() x2+
x2+![]() x)��4=-
x)��4=-![]() x2+
x2+![]() x.
x.
�൱x=2ʱ����EPC��������.
��P��2��-![]() ��.
��.
��3����ͼ����ʾ��
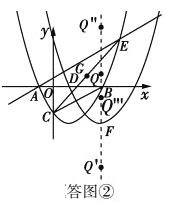
��y��������D��y���Ķ���Ϊ��F��
���F��3��-![]() ��.
��.
�ߵ�GΪCE���е㣬
��G��2��![]() ��.
��.
��FG=![]() ��.
��.
�൱FG=FQʱ����Q��3��![]() ����Q�䣨3��
����Q�䣨3��![]() ��.
��.
��GF=GQʱ����F���Q������y=![]() �Գƣ�
�Գƣ�
����Q�壨3��2![]() ��.
��.
��QG=QFʱ�����Q1�ĵ�����Ϊ��3��a��.
�������ľ��빫ʽ����֪����a+![]() =
=![]() �������a=-
�������a=-![]() .
.
���Q1��������3��-![]() ��.
��.
������������Q��������3��![]() ����3��
����3��![]() ����3��2
����3��2![]() ����3��-
����3��-![]() ��.
��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��QQ�˶���¼��С��ְ�2017��2�·�7�첽�еIJ�������λ�������±���
���� | 2��6�� | 2��7�� | 2��8�� | 2��9�� | 2��10�� | 2��11�� | 2��12�� |
���� | 2.1 | 1.7 | 1.8 | 1.9 | 2.0 | 1.8 | 2.0 |
��1�������ʵ���ͳ��ͼ��ʾС��ְ���7�첽�еIJ����ı仯���ƣ�
��2����С��ְ���7����ÿ�첽�е�ƽ��������
��3������С��ְ�2�·ݲ��е��ܲ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���ߡ��ˡ����꼶��ѧ����������ˮƽ���ԣ��ɼ�����Ϊ���㡢���á��ϸ��ϸ��ĸ��ȵڣ�Ϊ�˽���β��������ѧУ�������꼶�����ȡ200��ѧ���������ɼ�����ͳ�Ʒ�����������ݵ�ͳ��ͼ�������£�
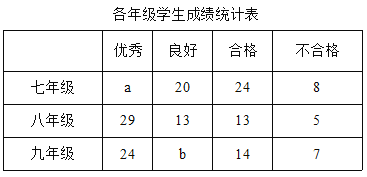

����������Ϣ����������⣺
��1����ͳ�Ʊ��У�a��ֵΪ��������������b��ֵΪ��������������
��2��������ͳ��ͼ�У����꼶����Ӧ������Բ�Ľ�Ϊ�������������ȣ�
��3������У�����꼶����2000��ѧ���μӿ��ԣ��Թ��Ƹ�Уѧ�������ɼ����ϸ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�������������ȱˮ�Ĺ���֮һ��Ϊ�˳�������Լ��ˮ������������С���������ڰ��50��ͬѧ�У����������10��ͬѧ��ͥ��һ����¾���ˮ������λ��t����������������������µ�����ͳ��ͼ
��1������10���������ݵ�ƽ��������������λ����
��2�������������ݣ�����С�����ڰ�50��ͬѧ��ͥ���¾���ˮ��������7 t��Լ�ж��ٻ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������M��O��N��Ӧ�����ֱ�Ϊ��1��0��3����PΪ����������һ�������Ӧ����Ϊx��
![]()
��1��MN�ij�Ϊ ��
��2�������P����M����N�ľ����������ôx��ֵ�� ��
��3���������Ƿ���ڵ�P��ʹ��P����M����N�ľ���֮����8����������ֱ��д��x��ֵ��������������˵��������
��4�������P��ÿ����1����λ���ȵ��ٶȴӵ�O�����˶���ͬʱ��M�͵�N�ֱ���ÿ����2����λ���Ⱥ�ÿ����3����λ���ȵ��ٶ�Ҳ�����˶�����t����ʱ��P����M����N�ľ����������t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABCD�У���E��BC���е㣬����AE���ӳ���DC���ӳ����ڵ�F������BF��
(1)��֤����ABE�ա�FCE��
(2)��AF��AD����֤���ı���ABFC�Ǿ��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڵ�������ABCD�У�AD//BC��E��AB���е㣬����E��EF//BC��CD�ڵ�F��AB��4��BC��6����B��60����
��1�����E��BC�ľ��룻
��2����PΪ�߶�EF�ϵ�һ�����㣬����P��PM��EF��BC��M����M��MN//AB������ADC��N������PN����EP��x��
�ٵ���N���߶�AD��ʱ����ͼ2������PMN����״�Ƿ����ı䣿�����䣬�����PMN���ܳ������ı䣬��˵�����ɣ�
�ڵ���N���߶�DC��ʱ����ͼ3�����Ƿ���ڵ�P��ʹ��PMNΪ���������Σ������ڣ��������������������x��ֵ���������ڣ���˵�����ɣ�



ͼ1 ͼ2 ͼ3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ϵ�A��B����ֱ��Ӧ����a��b����a��b����|4a-b|+��a-4��2=0
![]()
��1��a= ��b= ���������������A��B���㣻
��2������P�ӵ�A��������ÿ��3����λ������x���������˶������˶�ʱ��Ϊ����ʱ����P����A�ľ����ǵ�P����B�����2����
��3�������ϻ���һ��C������Ϊ30������P�͵�Qͬʱ�ӵ�A�͵�B�������ֱ���ÿ��3����λ���Ⱥ�ÿ��1����λ���ȵ��ٶ���C���˶���P�㵽��C�����������ͬ�����ٶȷ��أ��˶����յ�A�����P�͵�Q�˶�������ʱ��P��Q����֮��ľ���Ϊ4�������ʱ��Q��Ӧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ�У�OΪ����ԭ�㣬��֪A��-1��1��������������ȷ����P��ʹ��AOPΪ���������Σ�����������ĵ�P�ĸ������У���������
A. 10�� B. 8�� C. 4�� D. 6��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com