
【题目】QQ运动记录的小莉爸爸2017年2月份7天步行的步数(单位:万步)如下表:
日期 | 2月6日 | 2月7日 | 2月8日 | 2月9日 | 2月10日 | 2月11日 | 2月12日 |
步数 | 2.1 | 1.7 | 1.8 | 1.9 | 2.0 | 1.8 | 2.0 |
(1)制作适当的统计图表示小莉爸爸这7天步行的步数的变化趋势;
(2)求小莉爸爸这7天中每天步行的平均步数;
(3)估计小莉爸爸2月份步行的总步数.
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△AEC和△DFB中,∠E=∠F,点A,B,C,D在同一直线上,有如下三个关系式:①AE∥DF,②AB=CD,③CE=BF.

(1)请用其中两个关系式作为条件,另一个作为结论,写出你认为正确的所有命题(用序号写出命题书写形式:“如果,,那么”);
(2)选择(1)中你写出的一个命题,说明它正确的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,甲、乙两个容器内都装了一定数量的水,现将甲容器中的水匀速注入乙容器中.图2中的线段AB,CD分别表示容器中的水的深度h(厘米)与注入时间t(分钟)之间的函数图象.下列结论错误的是( )
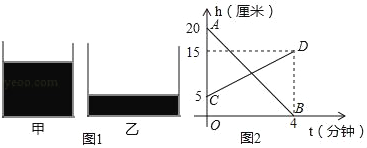
A. 注水前乙容器内水的高度是5厘米
B. 甲容器内的水4分钟全部注入乙容器
C. 注水2分钟时,甲、乙两个容器中的水的深度相等
D. 注水1分钟时,甲容器的水比乙容器的水深5厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
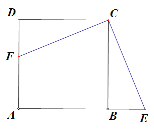
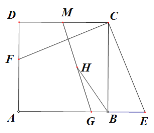
【题目】如图,四边形ABCD是正方形,在AB的延长线上取一点E,连接EC,过点C作CF⊥EC交AD于F.
(1)求证:EC=FC.
(2)若G、M分别是AB、CD上一动点,连接GM.H是GM上的中点,连接BH,当G、M运动到某一特殊位置时得到BH=BG +CM,此时∠ABH的度数是多少?请说明理由.
(3)在(2)的条件下,若BG=1,MC=![]() ,连接AH.求出四边形AHMD的面积.
,连接AH.求出四边形AHMD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形.
(1)如图(1),点E在线段AB上,点D在射线CB上,且ED=EC.将△BCE绕点C顺时针旋转60°至△ACF,连接EF.猜想线段AB,DB,AF之间的数量关系;
(2)点E在线段BA的延长线上,其它条件与(1)中一致,请在图(2)的基础上将图形补充完整,并猜想线段AB,DB,AF之间的数量关系;
(3)请选择(1)或(2)中的一个猜想进行证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】指出下列近似数精确到哪个数位:
(1)π≈3.14 精确到______. (2)![]() 精确到____;
精确到____;
(3)21.80≈______(精确到个位);(4)579700 精确到千位是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
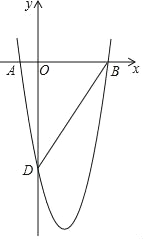
【题目】如图,二次函数y=ax2+bx﹣4![]() 的图象经过A(﹣1,0)、B(4,0)两点,于y轴交于点D.
的图象经过A(﹣1,0)、B(4,0)两点,于y轴交于点D.
(1)求这个二次函数的表达式;
(2)已知点C(3,m)在这个二次函数的图象上,连接BC,点P为抛物线上一点,且∠CBP=60°.
①求∠OBD的度数;
②求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
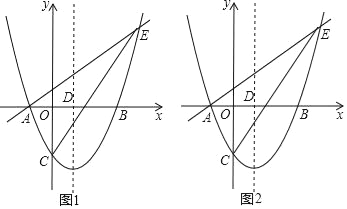
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,求P点坐标?
(3)点G是线段CE的中点,将抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com