
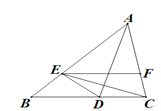
【题目】如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②EC平分∠DEF;③AD垂直平分CE.其中结论正确的有( )个
A. 1 B. 2 C. 3 D. 0
【答案】C
【解析】根据角平分线的定义可得∠BAD=∠CAD,然后利用“边角边”证明△ADC和△ADE全等,根据全等三角形对应边相等可得CD=DE,根据等边对等角可得∠CED=∠ECD,再根据两直线平行,内错角相等可得∠ECD=∠CEF,然后求出∠CED=∠CEF,再根据角平分线的定义判断出CE平分∠DEF,然后根据到线段两端点距离相等的点在线段的垂直平分线上判断出AD垂直平分CE.
∵AD是角平分线,
∴∠BAD=∠CAD,
在△ADC和△ADE中,
 ,
,
∴△ADC≌△ADE(SAS),故①正确;
∴CD=DE,
∴∠CED=∠ECD,
∵EF∥BC,
∴∠ECD=∠CEF,
∴∠CED=∠CEF,
∴CE平分∠DEF,故②正确;
∵AE=AC,CD=DE,
∴AD垂直平分CE,故③正确;
综上所述,正确的是①②③.
故选:C.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
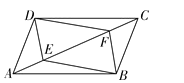
【题目】如图,点 E,F 是ABCD 对角线上两点,在条件①DE=BF;②∠ADE=∠CBF; ③AF=CE;④∠AEB=∠CFD 中,添加一个条件,使四边形 DEBF 是平行四边形,可添加 的条件是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E,连接AG.
(1)求证:AG=CG;
(2)求证:AG2=GE·GF.

查看答案和解析>>
科目:初中数学 来源: 题型:
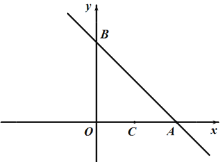
【题目】如图,直线y=-x+4分别与x轴、y轴交于A、B两点.
(1)求A、B两点的坐标;
(2)已知点C坐标为(2,0),设点C关于直线AB的对称点为D,请直接写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)点B表示的数是_____;
(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.当点P运动_____秒时,点P与点Q间的距离为8个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1 , x2 , 其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b<0,b2+8a>4ac,a<﹣1,其中结论正确的有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )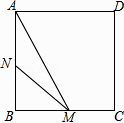
A.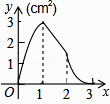
B.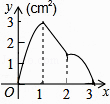
C.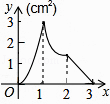
D.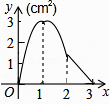
查看答案和解析>>
科目:初中数学 来源: 题型:
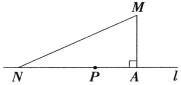
【题目】如图,一学校(点M)距公路(直线l)的距离(MA)为1km,在公路上距该校2km处有一车站(点N),该校拟在公路上建一个公交车停靠点(点p),以便于本校职工乘车上下班,要求停靠站建在AN之间且到此校与车站的距离相等,请你计算停靠站到车站的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E. 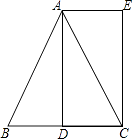
(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com