
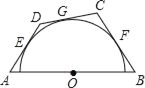
【题目】如图,AB是定长线段,圆心O是AB的中点,AE、BF为切线,E、F为切点,满足AE=BF,在![]() 上取动点G,国点G作切线交AE、BF的延长线于点D、C,当点G运动时,设AD=y,BC=x,则y与x所满足的函数关系式为( )
上取动点G,国点G作切线交AE、BF的延长线于点D、C,当点G运动时,设AD=y,BC=x,则y与x所满足的函数关系式为( )
A. 正比例函数y=kx(k为常数,k≠0,x>0)
B. 一次函数y=kx+b(k,b为常数,kb≠0,x>0)
C. 反比例函数y=![]() (k为常数,k≠0,x>0)
(k为常数,k≠0,x>0)
D. 二次函数y=ax2+bx+c(a,b,c为常数,a≠0,x>0)
【答案】C
【解析】
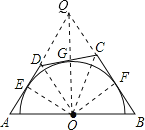
延长AD,BC交于点Q,连接OE,OF,OD,OC,OQ,由AE与BF为圆的切线,利用切线的性质得到AE与EO垂直,BF与OF垂直,由AE=BF,OE=OF,利用HL得到直角三角形AOE与直角BOF全等,利用全等三角形的对应角相等得到∠A=∠B,利用等角对等边可得出三角形QAB为等腰三角形,由O为底边AB的中点,利用三线合一得到QO垂直于AB,得到一对直角相等,再由∠FQO与∠OQB为公共角,利用两对对应角相等的两三角形相似得到三角形FQO与三角形OQB相似,同理得到三角形EQO与三角形OAQ相似,由相似三角形的对应角相等得到∠QOE=∠QOF=∠A=∠B,再由切线长定理得到OD与OC分别为∠EOG与∠FOG的平分线,得到∠DOC为∠EOF的一半,即∠DOC=∠A=∠B,又∠GCO=∠FCO,得到三角形DOC与三角形OBC相似,同理三角形DOC与三角形DAO相似,进而确定出三角形OBC与三角形DAO相似,由相似得比例,将AD=x,BC=y代入,并将AO与OB换为AB的一半,可得出x与y的乘积为定值,即y与x成反比例函数,即可得到正确的选项.
延长AD,BC交于点Q,连接OE,OF,OD,OC,OQ,
∵AE,BF为圆O的切线,
∴OE⊥AE,OF⊥FB,
∴∠AEO=∠BFO=90°,
在Rt△AEO和Rt△BFO中,
∵![]() ,
,
∴Rt△AEO≌Rt△BFO(HL),
∴∠A=∠B,
∴△QAB为等腰三角形,
又∵O为AB的中点,即AO=BO,
∴QO⊥AB,
∴∠QOB=∠QFO=90°,
又∵∠OQF=∠BQO,
∴△QOF∽△QBO,
∴∠B=∠QOF,
同理可以得到∠A=∠QOE,
∴∠QOF=∠QOE,
根据切线长定理得:OD平分∠EOG,OC平分∠GOF,
∴∠DOC=![]() ∠EOF=∠A=∠B,
∠EOF=∠A=∠B,
又∵∠GCO=∠FCO,
∴△DOC∽△OBC,
同理可以得到△DOC∽△DAO,
∴△DAO∽△OBC,
∴![]() ,
,
∴ADBC=AOOB=![]() AB2,即xy=
AB2,即xy=![]() AB2为定值,
AB2为定值,
设k=![]() AB2,得到y=
AB2,得到y=![]() ,
,
则y与x满足的函数关系式为反比例函数y=![]() (k为常数,k≠0,x>0).
(k为常数,k≠0,x>0).
故选:C.


科目:初中数学 来源: 题型:
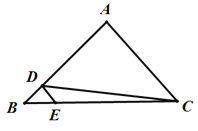
【题目】如图,在△ABC中,D,E分别是AB,BC边上的点,且DE∥AC,若![]() ,
,![]() ,则△ACD的面积为( )
,则△ACD的面积为( )
A. 64 B. 72 C. 80 D. 96
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长为15m的梯子斜靠在墙上,梯子的顶端距地面的距离为12m,
①如果梯子的顶端下滑了1m,那么梯子的底端也向后滑动1m吗?请通过计算解答.
②梯子的顶端从A处沿墙AO下滑的距离与点B向外移动的距离有可能相等吗?若有可能,请求出这个距离,没有可能请说明理由.
③若将上题中的梯子换成15米长的直木棒,将木棒紧靠墙竖直放置然后开始下滑直至直木棒的顶端A滑至墙角O处,试求出木棒的中点Q滑动的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,如果由甲队单独做这项工程刚好如期完成,若乙队单独做这项工程,要比规定日期多5天完成.现由若甲、乙两队合作4天后,余下的工程由乙队单独做,也正好如期完成.已知甲、乙两队施工一天的工程费分别为16万元和14万元.
(1)求规定如期完成的天数.
(2)现有两种施工方案:方案一:由甲队单独完成;方案二:先由甲、乙合作4天,再由乙队完成其余部分;通过计算说明,哪一种方案比较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】跳远运动员李阳对训练效果进行测试.6次跳远的成绩如下:7.5,7.7,7.6,7.7,7.9,7.8(单位:m)这六次成绩的平均数为7.7m,方差为![]() .如果李阳再跳一次,成绩为7.7m.则李阳这7次跳远成绩的方差_____(填“变大”、“不变”或“变小”).
.如果李阳再跳一次,成绩为7.7m.则李阳这7次跳远成绩的方差_____(填“变大”、“不变”或“变小”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,△ACE是等腰三角形,∠AEC=120°,AE=CE,F为BC中点,连接AE.
(1)直接写出∠BAE的度数为 ;
(2)判断AF与CE的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:
![]() 是一个无理数,而无理数是无限不循环小数,因此
是一个无理数,而无理数是无限不循环小数,因此![]() 的小数部分无法全部写出来,但是我们可以想办法把它表示出来.因为
的小数部分无法全部写出来,但是我们可以想办法把它表示出来.因为![]() ,所以
,所以![]() 的整数部分为
的整数部分为![]() ,将
,将![]() 减去其整数部分后,得到的差就是小数部分,于是
减去其整数部分后,得到的差就是小数部分,于是![]() 的小数部分为
的小数部分为![]() .
.
(1)求出![]() 的整数部分和小数部分:
的整数部分和小数部分:
(2)求出![]() 的整数部分和小数部分;
的整数部分和小数部分;
(3)如果![]() 的整数部分是
的整数部分是![]() ,小数部分是
,小数部分是![]() ,求出
,求出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com