
 如图,在正方形ABCD中,E在BC上,P在BD上,已知PA=PE,求证:PA⊥PE.
如图,在正方形ABCD中,E在BC上,P在BD上,已知PA=PE,求证:PA⊥PE. 分析 作PQ⊥AB于Q,作PK⊥BC于K,则四边形BQPK是矩形,得出∠QPK=90°,由正方形的性质得出BD平分∠ABC,得出PQ=PK,由HL证明Rt△APQ≌Rt△EPK,得出∠APQ=∠EPK,由角的互余关系证出∠APE=90°,即可得出结论.
解答 证明:作PQ⊥AB于Q,作PK⊥BC于K,如图所示: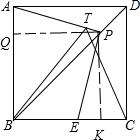
则四边形BQPK是矩形,
∴∠QPK=90°,即∠QPE+∠EPK=90°,
∵四边形ABCD是正方形,
∴BD平分∠ABC,
∴PQ=PK,
在Rt△APQ和Rt△EPK中,
$\left\{\begin{array}{l}{PA=PE}\\{PQ=PK}\end{array}\right.$,
∴Rt△APQ≌Rt△EPK(HL),
∴∠APQ=∠EPK,
∴∠APQ+∠QPE=90°,
即∠APE=90°,
∴AP⊥PE
点评 本题考查了正方形的性质、全等三角形的判定与性质;熟练掌握正方形的性质,并能进行推理论证与计算是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
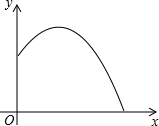 如图是某运动员打羽毛球的抛物线示意图,已知打出羽毛球的高度y(m)与水平距离x(m)之间的函数关系式是y=-$\frac{1}{2}$x2+$\frac{5}{2}$x+7,则该羽毛球落地时距离发出点( )
如图是某运动员打羽毛球的抛物线示意图,已知打出羽毛球的高度y(m)与水平距离x(m)之间的函数关系式是y=-$\frac{1}{2}$x2+$\frac{5}{2}$x+7,则该羽毛球落地时距离发出点( )| A. | 6m | B. | 7m | C. | 8m | D. | 9m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
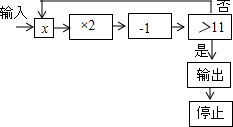 如图为某一运算程序,规定:程序运行到判断“结果是否大于11”为一次运算,若输入整数x后,运算进行了2次就输出停止,则满足条件的整数x是4、5或6.
如图为某一运算程序,规定:程序运行到判断“结果是否大于11”为一次运算,若输入整数x后,运算进行了2次就输出停止,则满足条件的整数x是4、5或6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
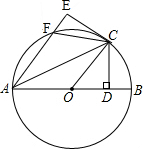 如图,AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于D.△ACD沿AC翻折后点D落在点E,AE交⊙O于点F;连接OC、FC.
如图,AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于D.△ACD沿AC翻折后点D落在点E,AE交⊙O于点F;连接OC、FC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,铁路上A,B两站(视为直线上两点)相距14km,C,D为两村庄(可看为两个点),DA⊥AB于A,CB⊥AB于B,已知DA=8km,CB=6km,现要在铁路上建一个土特产品收购站E,使C,D两村到E站的距离相等,则E站应建在距A站多少km处?
如图所示,铁路上A,B两站(视为直线上两点)相距14km,C,D为两村庄(可看为两个点),DA⊥AB于A,CB⊥AB于B,已知DA=8km,CB=6km,现要在铁路上建一个土特产品收购站E,使C,D两村到E站的距离相等,则E站应建在距A站多少km处?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com