
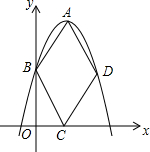
 如图,在平面直角坐标系中,抛物线y=ax2-2ax+$\frac{3}{2}$(a<0)的顶点为A,与y轴的交点为B,点B关于抛物线对称轴的对称点为D,四边形ABCD为菱形,若点C在x轴上,则a的值为-$\frac{3}{2}$.
如图,在平面直角坐标系中,抛物线y=ax2-2ax+$\frac{3}{2}$(a<0)的顶点为A,与y轴的交点为B,点B关于抛物线对称轴的对称点为D,四边形ABCD为菱形,若点C在x轴上,则a的值为-$\frac{3}{2}$. 分析 把二次函数解析式整理成顶点式形式,然后写出点A的坐标,再求出点B的坐标,然后根据菱形的轴对称性,点A的纵坐标等于点B的纵坐标的2倍列方程求解即可.
解答 解:∵y=ax2-2ax+$\frac{3}{2}$=a(x-1)2-a+$\frac{3}{2}$,
∴顶点A的坐标为(1,-a+$\frac{3}{2}$),
令x=0,则y=$\frac{3}{2}$,
所以,点B的坐标为(0,$\frac{3}{2}$),
∵点B关于抛物线对称轴的对称点为D,四边形ABCD为菱形,
∴-a+$\frac{3}{2}$=2×$\frac{3}{2}$,
解得a=-$\frac{3}{2}$.
故答案为:-$\frac{3}{2}$.
点评 本题考查了菱形的轴对称性,二次函数的性质,解题的关键在于确定出点A的纵坐标等于点B的纵坐标的2倍.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 32 | B. | 64 | C. | 128 | D. | 256 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1×107 | B. | 0.1×107 | C. | 1×106 | D. | 10×101 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
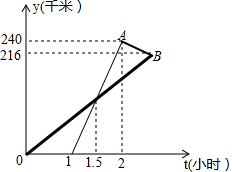 十一期间,小明和小亮相约从长春出发到某市某游乐园游玩,小明乘私家车从长春出发1小时后,小亮乘“和谐号”动车从长春出发,先到某市火车站A,然后乘出租车去游乐园B(换车时间忽略不计),两人恰好同时到达游乐园,他们离开长春的距离y(千米)与小明乘车时间t(时)的函数图象如图所示.
十一期间,小明和小亮相约从长春出发到某市某游乐园游玩,小明乘私家车从长春出发1小时后,小亮乘“和谐号”动车从长春出发,先到某市火车站A,然后乘出租车去游乐园B(换车时间忽略不计),两人恰好同时到达游乐园,他们离开长春的距离y(千米)与小明乘车时间t(时)的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
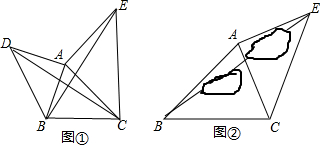
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com