
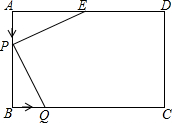
 如图,已知矩形(即小学学过的长方形)ABCD中,AD=6cm,AB=4cm,点E为AD的中点.
如图,已知矩形(即小学学过的长方形)ABCD中,AD=6cm,AB=4cm,点E为AD的中点.分析 (1)①当t=1时,AP=BQ,∠A=∠B,AE=PB,从而可证明△EAP≌Rt△PBQ;②如图1所示连接QE.当t≤4时,AP=BQ=t,S=S梯形AEQB-SAEP-SPBQ;当4<t≤6时,点P与点B重合,S=$\frac{1}{2}QB•AB$=$\frac{1}{2}×4×t$=2t;③如图3所示:因为△AEP≌△BQP,所以AP=PB=2,AE=BQ=3,从而可求得t=2,点Q运动的速度为=3÷2=1.5cm/秒;
(2)设运动时间为t秒时,第一次相遇.根据题意得;1.5t-t=16.解得t=32,从而可确定出点P和点Q经过32秒在DC上第一次相遇.
解答 解:(1)①当t=1时,AP=1,BQ=1,
∴AP=BQ.
∵E是AD的中点,
∴AE=$\frac{1}{2}AD=\frac{1}{2}×6=3$.
∵PB=AB=AP=4-1=3,
∴AE=PB.
在Rt△EAP和Rt△PBQ中,$\left\{\begin{array}{l}{AE=PB}\\{∠A=∠B}\\{AP=BQ}\end{array}\right.$,
∴△EAP≌Rt△PBQ.
②如图1所示连接QE.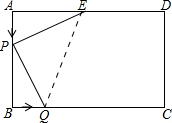
图1
当t≤4时,AP=BQ=t,
S梯形AEQB=$\frac{1}{2}(AE+BQ)•AB$=$\frac{1}{2}×4×(3+t)$=2t+6.
${S}_{△AEP}=\frac{1}{2}AE•PA=\frac{1}{2}×3t$=$\frac{3}{2}t$,${S}_{△PBQ}=\frac{1}{2}PB•BQ$=$\frac{1}{2}×(4-t)t$=2t-$\frac{1}{2}{t}^{2}$.
∴S=2t+6-$\frac{3}{2}t$-($2t-\frac{1}{2}{t}^{2}$).
整理得:S=$\frac{1}{2}{t}^{2}-\frac{3}{2}t+6$,
如图2所示: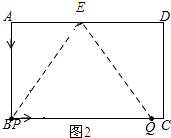
当4<t≤6时,点P与点B重合,
S=$\frac{1}{2}QB•AB$=$\frac{1}{2}×4×t$=2t.
∴S与t的函数关系式为S=$\left\{\begin{array}{l}{\frac{1}{2}{t}^{2}-\frac{3}{2}t+6(0≤t≤4)}\\{2t(4<t≤6)}\end{array}\right.$;
③如图3所示: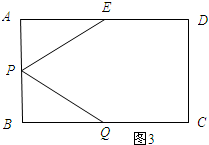
∵△AEP≌△BQP,PA≠BQ,
∴AP=PB=2,AE=BQ=3.
∴t=AP=$\frac{1}{2}AB=\frac{1}{2}×4=2$.
∴点Q运动的速度为=3÷2=1.5cm/秒时,△AEP≌△BQP;
(2)设运动时间为t秒时,第一次相遇.
根据题意得1.5t-t=16.
解得t=32.
点P32秒运动的路程=32cm,根据矩形各边长可知点P和点Q经过32秒在DC上第一次相遇.
点评 本题组要考查的是全等三角形的性质和判定、相似三角形的性质和判定、矩形的性质、函数的解析式、一元一次方程的综合应用,根据题意画出符合题意的图形是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
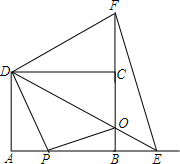 如图,矩形ABCD中,动点P从点A出发,沿线段AB以每秒2cm的速度向点B运动:同时动点Q从点B出发,沿线段BC以每秒1cm的速度向点C运动.当点P到达B点时,点Q同时停止,设运动时间为t秒.已知AD=6,且t=2时,PQ=2$\sqrt{5}$.
如图,矩形ABCD中,动点P从点A出发,沿线段AB以每秒2cm的速度向点B运动:同时动点Q从点B出发,沿线段BC以每秒1cm的速度向点C运动.当点P到达B点时,点Q同时停止,设运动时间为t秒.已知AD=6,且t=2时,PQ=2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
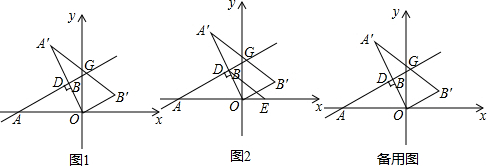
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com