
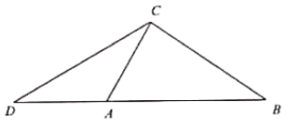
【题目】如图,已知在![]() 中,∠ACB=90°,
中,∠ACB=90°,![]() ,延长边BA至点D,使AD=AC,联结CD.
,延长边BA至点D,使AD=AC,联结CD.
(1)求∠D的正切值;
(2)取边AC的中点E,联结BE并延长交边CD于点F,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)过点C作CG⊥BD于G,根据已知三角函数值,设出参数表示出各边长,可求出CE,DE,进而可得出∠D的正切值.
(2)延长BF至H,使EH=BE,连接CH,则CH∥BD,![]() =
=![]() ,求出
,求出![]() 的值即可.
的值即可.
过点C作CG⊥BD于G,
∵![]() ,∴设AC=3a,则AB=5a,
,∴设AC=3a,则AB=5a,
易得∠ABC=∠ACG,∴sin∠ACG=![]() ,
,
∴AG=AC·sin∠ACG=![]() ,∴CG=
,∴CG=![]()
又AD=AC=3a,∴DG=AD+AG=![]()
∴tanD=![]() ,即∠D的正切值为
,即∠D的正切值为![]() .
.
延长BF至H,使EH=BE,连接CH,由CE=AE,则CH∥BD,
∴![]() =
=![]() ,△CEH≌△AEB,
,△CEH≌△AEB,
∴CH=AB=5a,
又BD=AD+AB=AE+AB=3a+5a=8a,
∴![]() =
=![]() =
=![]() .
.



科目:初中数学 来源: 题型:
【题目】甲、乙两台机器共同加工一批零件,一共用了![]() 小时.在加工过程中乙机器因故障停止工作,排除故障后,乙机器提高了工作效率且保持不变,继续加工.甲机器在加工过程中工作效率保持不变.甲、乙两台机器加工零件的总数
小时.在加工过程中乙机器因故障停止工作,排除故障后,乙机器提高了工作效率且保持不变,继续加工.甲机器在加工过程中工作效率保持不变.甲、乙两台机器加工零件的总数![]() (个)与甲加工时间
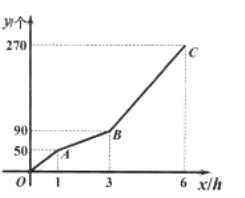
(个)与甲加工时间![]() 之间的函数图象为折线
之间的函数图象为折线![]() ,如图所示.
,如图所示.
(1)这批零件一共有 个,甲机器每小时加工 个零件,乙机器排除故障后每小时加工 个零件;
(2)当![]() 时,求
时,求![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
(3)在整个加工过程中,甲加工多长时间时,甲与乙加工的零件个数相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 如图所示,点
如图所示,点![]() 到
到![]() 、
、![]() 、
、![]() 三点的距离均等于
三点的距离均等于![]() (
(![]() 为常数),到点
为常数),到点![]() 的距离等于
的距离等于![]() 的所有点组成图形
的所有点组成图形![]() . 射线
. 射线![]() 与射线
与射线![]() 关于
关于![]() 对称,过点 C作
对称,过点 C作![]() 于
于![]() .
.
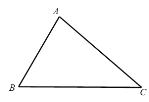
(1)依题意补全图形(保留作图痕迹);
(2)判断直线![]() 与图形
与图形![]() 的公共点个数并加以证明.
的公共点个数并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
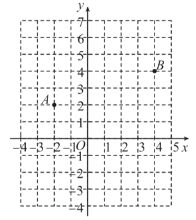
【题目】如图:在平面直角坐标系![]() 中,点
中,点![]() .
.
(1)尺规作图:求作过![]() 三点的圆;
三点的圆;
(2)设过![]() 三点的圆的圆心为M,利用网格,求点M的坐标;
三点的圆的圆心为M,利用网格,求点M的坐标;
(3)若直线![]() 与
与![]() 相交,直接写出
相交,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
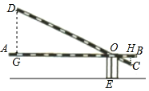
【题目】如图,某小区门口的栏杆从水平位置AB绕固定点O旋转到位置DC,已知栏杆AB的长为3.5米,OA的长为3米,点C到AB的距离为0.3米,支柱OE的高为0.6米,那么栏杆端点D离地面的距离为____________米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0),则下面的四个结论,其中正确的个数为( )
①2a+b=0②4a﹣2b+c<0③ac>0④当y>0时,﹣1<x<4
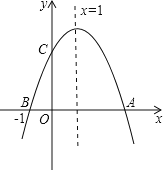
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是正方形,连接
是正方形,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得
得![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
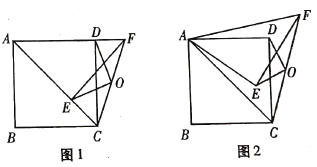
(1)如图1,当![]() 时,求证:
时,求证:![]() ;
;
(2)如图2,当![]() 时,(1)
时,(1)![]() 还成立吗?请说明理由.
还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BC=4,⊙P与△ABC的边或边的延长线相切.若⊙P半径为2,△ABC的面积为5,则△ABC的周长为( )
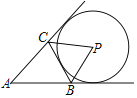
A.8B.10C.13D.14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com