
����Ŀ�����ǰ�һ����Բ����κ���ͼ���һ���ֺϳɵķ��ͼ�γ�Ϊ����Բ�������һ��ֱ���롰��Բ��ֻ��һ�����㣨��Բ����κ���ͼ������ӵ���⣩����ô����ֱ�߽�������Բ�������ߣ���ͼ�����κ���y=x2��2x��3��ͼ����x�ύ�ڵ�A��B����y�ύ�ڵ�D��ABΪ��Բֱ������ԲԲ��Ϊ��M����Բ��y��������ύ�ڵ�C��
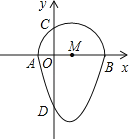
��1�����C�����ꣻ
��2���ֱ����������C�͵�D�ġ���Բ�������ߵı���ʽ��
���𰸡���1����0��![]() ������2��y=
������2��y=![]() x+
x+![]() ��y=��2x��3��
��y=��2x��3��
��������
�����������1������CM�������A��B�����꣬�����ɵõ�AB�ij�����Բ�İ뾶����������ɹ��ɶ��������OC�ij����̶��������C�����ꣻ
��2���ɣ�1����֪��C�����꣬�����C�ġ���Բ�������߽�x���ڵ�G��Ȼ������������������G�����꣬�ô���ϵ�������ֱ��GC�Ľ���ʽ����Ϊ������D�ġ���Բ�����߹�D�㣬���Ա���������Ľ���ʽΪy=kx��3������ͼ�����������ߵĽ���ʽ����Ϊ���У��������ǵĽ���ֻ��һ���������ɸ���һԪ���η��̵��й�֪ʶ������⣮
�⣺��1�������κ���y=x2��2x��3��ͼ����x�ύ�ڵ�A��B����y�ύ�ڵ�D��
����A����1��0������B�������ǣ�3��0����
��AB=4��
����ԲԲ��Ϊ��M��
��BM=AM=2��
��OM=1��
����CM��
��OC=![]() =
=![]() ��
��
����C�������ǣ�0��![]() ����
����
��2�������C�ġ���Բ�������߽�x���ڵ�G��
��GC����M�����ߣ�
���GCM=90����
��cos��OMC=![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��MG=4��
��G����3��0����
��ֱ��GC�ı���ʽΪy=![]() x+
x+![]() ��
��
�����D��ֱ�߱���ʽΪy=kx��3��
��![]() ��
��
��x2����2+k��x=0��
���=[����2+k��]2=0��
��k=��2��
������D�ġ���Բ�������ߵı���ʽΪy=��2x��3��
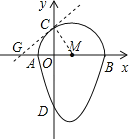


 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90������CAB=30������AB��Ϊһ������ABD����AD=BD����ADB=90�㣬ȡAB�е�E����DE��CE��CD������EDC= �㣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���ǣ���
A. ������Ա߷ֱ�ƽ�е��ı�����ƽ���ı���
B. ƽ���ı��εĶԽ�����ƽ��
C. ƽ���ı��εĶԱ�ƽ�������
D. ƽ���ı��εĶԽǻ������ڽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߶�AB=10������P�ӵ�A��������ÿ��1����λ���ٶȣ����߶�AB���յ�B�˶���ͬʱ����һ������Q�ӵ�B��������ÿ��3����λ���ٶ����߶�AB�������˶����ӵ�B���A�˶��������A������ԭ�ٷ��أ��ٴε���B���������ͷ���A�˶����� ����P����B��ʱ��P��Q���㶼ֹͣ�˶������P���˶�ʱ��Ϊx��
![]()
��1����x=3ʱ���߶�PQ�ij�Ϊ ��
��2����P��Q�����һ���غ�ʱ�����߶�BQ�ij���
��3���Ƿ����ijһʱ�̣�ʹ��Qǡ�������߶�AP���е��ϣ������ڣ��������������������x��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����λ������λ����Ϊa��ʮλ���ֱȸ�λ���ִ�1���������λ���ɱ�ʾΪ
A��11a��1 B��11a��10 C��11a��1 D��11a��10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������A��1����3����x������ƽ��3����λ���ȣ�����y������ƽ��5����λ���Ⱥ�õ��ĵ�A�������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ε����߳��ֱ�Ϊ5cm��10 cm����������ε��ܳ��ǣ� ��
A. 15 cm B. 20 cm C. 25 cm D. 20 cm��25 cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������100Ԫ������100Ԫ����ô֧��200Ԫ����
A����200Ԫ B����200Ԫ C����100Ԫ D����100Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Сѧ�������Ѿ������˽�������ε�ÿ���Ƕ���90�㣬ÿ���߶���ȣ���ͼ����������ABCD�����ֱ��AQ������QAD=30������D����ֱ��AQ�ĶԳƵ�ΪE������DE��BE��DE��AQ�ڵ�G��BE��AQ�ڵ�F��
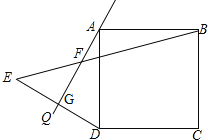
��1������ABE�Ķ�����
��2����AB=6����FG�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com