
【题目】如图,线段AB=10,动点P从点A出发,以每秒1个单位的速度,沿线段AB向终点B运动,同时,另一个动点Q从点B出发,以每秒3个单位的速度在线段AB上来回运动(从点B向点A运动,到达点A后,立即原速返回,再次到达B点后立即调头向点A运动.) 当点P到达B点时,P,Q两点都停止运动.设点P的运动时间为x.
![]()
(1)当x=3时,线段PQ的长为 .
(2)当P,Q两点第一次重合时,求线段BQ的长.
(3)是否存在某一时刻,使点Q恰好落在线段AP的中点上?若存在,请求出所有满足条件的x的值;若不存在,请说明理由.
【答案】(1)2;(2)7.5;(3)当x=![]() 或x=4或x=
或x=4或x=![]() 时,点Q恰好落在线段AP的中点上.
时,点Q恰好落在线段AP的中点上.
【解析】试题分析:(1)结合图形,表示出AP、AQ的长,可得PQ;
(2)当P,Q两点第一次重合时,点P运动路程+点Q运动路程=AB的长,列方程可求得;
(3)点Q落在线段AP的中点上有以下三种情况:①点Q从点B出发未到点A;②点Q到达点A后,从A到B;
③点Q第一次返回到B后,从B到A,根据AP=2AQ列方程可得.
解:(1)根据题意,当x=3时,P、Q位置如下图所示:
![]()
此时:AP=3,BQ=3×3=9,AQ=AB﹣BQ=10﹣9=1,
∴PQ=AP﹣AQ=2;
(2)设x秒后P,Q第一次重合,得:x+3x="10"
解得:x=2.5,
∴BQ=3x=7.5;
(3)设x秒后,点Q恰好落在线段AP的中点上,根据题意,
①当点Q从点B出发未到点A时,即0<x<![]() 时,有
时,有
x=2(10﹣3x),
解得![]() ;
;
②当点Q到达点A后,从A到B时,即![]() <x<
<x<![]() 时,有
时,有
x=2(3x﹣10),
解得 x=4;
③当点Q第一次返回到B后,从B到A时,即![]() <x<10时,有
<x<10时,有
x=2(30﹣3x),
解得![]() ;
;
综上所述:当x=![]() 或x=4或x=
或x=4或x=![]() 时,点Q恰好落在线段AP的中点上.
时,点Q恰好落在线段AP的中点上.
故答案为:(1)2.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
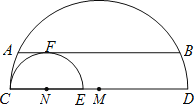
【题目】如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设![]() 、
、![]() 的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相交于A(2,3),B(﹣3,n)两点.
的图象相交于A(2,3),B(﹣3,n)两点.
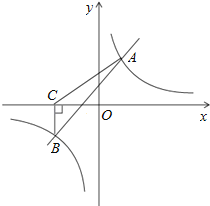
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A为⊙O外一点,AB切⊙O于点B,AO交⊙O于C,CD⊥OB于E,交⊙O于点D,连接OD.若AB=12,AC=8.
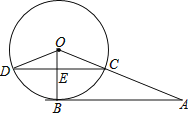
(1)求OD的长;
(2)求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋里有四个完全相同的小球,把它们分别标号为1,2,3,4,小明和小强采取的摸取方法分别是:
小明:随机摸取一个小球记下标号,然后放回,再随机摸取一个小球,记下标号;
小强:随机摸取一个小球记下标号,不放回,再随机摸取一个小球,记下标号.
(1)用画树状图(或列表法)分别表示小明和小强摸球的所有可能出现的结果;
(2)分别求出小明和小强两次摸球的标号之和等于5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把一个半圆与二次函数图象的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点(半圆与二次函数图象的连接点除外),那么这条直线叫做“蛋圆”的切线.如图,二次函数y=x2﹣2x﹣3的图象与x轴交于点A、B,与y轴交于点D,AB为半圆直径,半圆圆心为点M,半圆与y轴的正半轴交于点C.
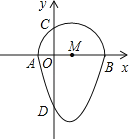
(1)求点C的坐标;
(2)分别求出经过点C和点D的“蛋圆”的切线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=mx2﹣(m+1)x+1.
(1)求证:该抛物线与x轴总有交点;
(2)若m为整数,当一元二次方程mx2﹣(m+1)x+1=0的根都是整数时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、B、D三点在同一直线上,BM为∠CBE的平分线,BN为∠DBE的平分线,则∠MBN的度数是( )
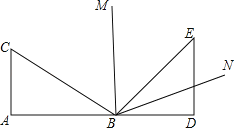
A.60° B.67.5° C.75° D.85°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com