
����Ŀ����һ���ڴ������ĸ���ȫ��ͬ��С�����Ƿֱ���Ϊ1��2��3��4��С����Сǿ��ȡ����ȡ�����ֱ��ǣ�
С���������ȡһ��С����±�ţ�Ȼ��Żأ��������ȡһ��С���±�ţ�
Сǿ�������ȡһ��С����±�ţ����Żأ��������ȡһ��С���±�ţ�
��1���û���״ͼ�����б������ֱ��ʾС����Сǿ��������п��ܳ��ֵĽ����
��2���ֱ����С����Сǿ��������ı��֮�͵���5�ĸ��ʣ�
���𰸡���1������������2��P��С����������ı��֮�͵���5��=![]() ��P��Сǿ��������ı��֮�͵���5��=
��P��Сǿ��������ı��֮�͵���5��=![]() ��
��
��������
�����������1�����ȸ������⻭����״ͼ��Ȼ������״ͼ�ó����п��ܵĽ����ע���ǷŻ�ʵ�黹�Dz��Ż�ʵ�飻
��2�����ݣ�1�������С����������ı��֮�͵���5����4�ֿ��ܣ�Сǿ��������ı��֮�͵���5����4�ֿ��ܣ�Ȼ�����ø��ʹ�ʽ��⼴����ô𰸣�
�⣺��1������״ͼ�ã�
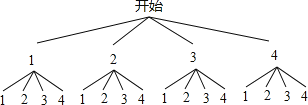
��С������16�ֵȿ��ܵĽ����

��Сǿ����12�ֵȿ��ܵĽ����
��2����С����������ı��֮�͵���5����4�ֿ��ܣ�Сǿ��������ı��֮�͵���5����4�ֿ��ܣ�
��P��С����������ı��֮�͵���5��=![]() =
=![]() ��
��
P��Сǿ��������ı��֮�͵���5��=![]() =
=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ÿ�ѧ��������ʾ0.00001032��������ȷ���ǣ� ��
A. 0.1032��10-4 B. 1.032��103 C. 10.32��10-6 D. 1.032��10-5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ���ABC�߳�Ϊ2������P�ӵ�A��������ÿ��1����λ���ȵ��ٶȣ���A��B��C��A�ķ����˶��������Aʱֹͣ�����˶�ʱ��Ϊx�룬y=PC����y����x������ͼ�����Ϊ�� ��

A��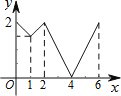 B��
B��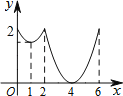
C��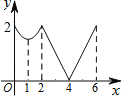 D��
D��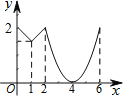
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ1��С��������ɵķ���ֽ�У���һ���Ը��Ϊ�������ABC��
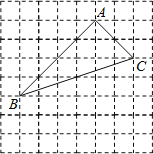
��1���Ը������������߹�ϵ���ж���ABC����״��
��2���ڷ���ֽ������ֱ�߷ֱ�AB��BC�Ĵ�ֱƽ���ߣ�����ΪO���۲��O��λ�ã����ܵó������Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߶�AB=10������P�ӵ�A��������ÿ��1����λ���ٶȣ����߶�AB���յ�B�˶���ͬʱ����һ������Q�ӵ�B��������ÿ��3����λ���ٶ����߶�AB�������˶����ӵ�B���A�˶��������A������ԭ�ٷ��أ��ٴε���B���������ͷ���A�˶����� ����P����B��ʱ��P��Q���㶼ֹͣ�˶������P���˶�ʱ��Ϊx��
![]()
��1����x=3ʱ���߶�PQ�ij�Ϊ ��
��2����P��Q�����һ���غ�ʱ�����߶�BQ�ij���
��3���Ƿ����ijһʱ�̣�ʹ��Qǡ�������߶�AP���е��ϣ������ڣ��������������������x��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У���P����2��3������x��ԳƵĵ������Ϊ�� ��
A������2����3�� B����2����3�� C������3����2�� D����3����2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������A��1����3����x������ƽ��3����λ���ȣ�����y������ƽ��5����λ���Ⱥ�õ��ĵ�A�������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ��Ī����1925�귢���������ϵ�һ�����������Σ���ͼ��һ�����������Σ���ǡ�ܱ��ָ��10����С��ͬ�������Σ����б�ע����1�������α߳�Ϊ5����������������ε����Ϊ ��
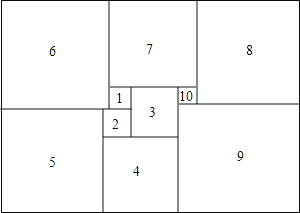
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=��![]() x2+bx+c��������ֱ��ڵ�A��0��8����B��8��0���͵�E������C��ԭ��O��ʼ��OA������ÿ��1����λ�����ƶ�������D�ӵ�B��ʼ��BO������ÿ��1����λ�����ƶ�������C��Dͬʱ������������D����ԭ��Oʱ����C��Dֹͣ�˶���
x2+bx+c��������ֱ��ڵ�A��0��8����B��8��0���͵�E������C��ԭ��O��ʼ��OA������ÿ��1����λ�����ƶ�������D�ӵ�B��ʼ��BO������ÿ��1����λ�����ƶ�������C��Dͬʱ������������D����ԭ��Oʱ����C��Dֹͣ�˶���

��1��ֱ��д�������ߵĽ���ʽ�� ��
��2������CED�����S��D���˶�ʱ��t�ĺ�������ʽ����tΪ��ֵʱ����CED���������������Ƕ��٣�
��3������CED��������ʱ�������������Ƿ���ڵ�P����E���⣩��ʹ��PCD�����������CED���������������ڣ����P������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com