
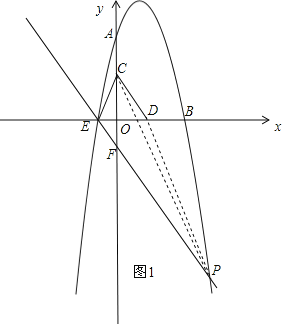
����Ŀ����ͼ����֪������y=��![]() x2+bx+c��������ֱ��ڵ�A��0��8����B��8��0���͵�E������C��ԭ��O��ʼ��OA������ÿ��1����λ�����ƶ�������D�ӵ�B��ʼ��BO������ÿ��1����λ�����ƶ�������C��Dͬʱ������������D����ԭ��Oʱ����C��Dֹͣ�˶���
x2+bx+c��������ֱ��ڵ�A��0��8����B��8��0���͵�E������C��ԭ��O��ʼ��OA������ÿ��1����λ�����ƶ�������D�ӵ�B��ʼ��BO������ÿ��1����λ�����ƶ�������C��Dͬʱ������������D����ԭ��Oʱ����C��Dֹͣ�˶���

��1��ֱ��д�������ߵĽ���ʽ�� ��
��2������CED�����S��D���˶�ʱ��t�ĺ�������ʽ����tΪ��ֵʱ����CED���������������Ƕ��٣�
��3������CED��������ʱ�������������Ƿ���ڵ�P����E���⣩��ʹ��PCD�����������CED���������������ڣ����P������ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=��![]() x2+3x+8����2����t=5ʱ��S���=
x2+3x+8����2����t=5ʱ��S���=![]() ����3������CED��������ʱ�����������ϴ��ڵ�P����E���⣩��ʹ��PCD�����������CED������������P������Ϊ��P��
����3������CED��������ʱ�����������ϴ��ڵ�P����E���⣩��ʹ��PCD�����������CED������������P������Ϊ��P��![]() ����
����![]() ����P��8��0����P��
����P��8��0����P��![]() ��
��![]() ����
����
��������
�����������1������A��0��8����B��8��0������������y=��![]() x2+bx+c������������ߵĽ���ʽΪ��y=��
x2+bx+c������������ߵĽ���ʽΪ��y=��![]() x2+3x+8��
x2+3x+8��
��2����������ã���D���˶�t��ʱ��BD=t��OC=t��Ȼ���ɵ�A��0��8����B��8��0�����ɵ�OA=8��OB=8���Ӷ��ɵ�OD=8��t��Ȼ����y=0�������E������Ϊ����2��0���������ɵ�OE=2��DE=2+8��t=10��t��Ȼ�����������ε������ʽ��������CED�����S��D���˶�ʱ��t�ĺ�������ʽΪ��S=��![]() t2+5t��Ȼ��ת��Ϊ����ʽ���������ֵΪ��S���=
t2+5t��Ȼ��ת��Ϊ����ʽ���������ֵΪ��S���=![]() ��
��
��3���ɣ�2��֪����t=5ʱ��S���=![]() ��������֪����t=5ʱ��OC=5��OD=3�������ɵ�CD=
��������֪����t=5ʱ��OC=5��OD=3�������ɵ�CD=![]() ���Ӷ�ȷ��C��0��5����D��3��0��Ȼ����ݴ���ϵ�������ֱ��CD�Ľ���ʽΪ��y=��
���Ӷ�ȷ��C��0��5����D��3��0��Ȼ����ݴ���ϵ�������ֱ��CD�Ľ���ʽΪ��y=��![]() x+5��Ȼ���E����EF��CD�������������P��Ȼ�����ֱ��EF�Ľ���ʽ���������������������ü��ɵõ����е�һ����P�����꣬Ȼ����������������E��CD�ľ���Ϊ��
x+5��Ȼ���E����EF��CD�������������P��Ȼ�����ֱ��EF�Ľ���ʽ���������������������ü��ɵõ����е�һ����P�����꣬Ȼ����������������E��CD�ľ���Ϊ��![]() ��Ȼ�����D��DN��CD������ΪN����ʹDN=
��Ȼ�����D��DN��CD������ΪN����ʹDN=![]() ��Ȼ�����N�����꣬Ȼ�����N��NH��CD���������߽����P��Ȼ�����ֱ��NH�Ľ���ʽ����������������������⼴�ɵõ����е���������P�����꣮
��Ȼ�����N�����꣬Ȼ�����N��NH��CD���������߽����P��Ȼ�����ֱ��NH�Ľ���ʽ����������������������⼴�ɵõ����е���������P�����꣮
�⣺��1������A��0��8����B��8��0������������y=��![]() x2+bx+c�ã�
x2+bx+c�ã�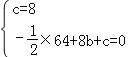 ��
��
��ã�b=3��c=8��
�������ߵĽ���ʽΪ��y=��![]() x2+3x+8��
x2+3x+8��
�ʴ�Ϊ��y=��![]() x2+3x+8��
x2+3x+8��
��2������A��0��8����B��8��0����
��OA=8��OB=8��
��y=0�����![]() x2+3x+8=0��
x2+3x+8=0��
��ã�x18��x2=2��
����E��x��ĸ������ϣ�
����E����2��0����
��OE=2��
��������ã���D���˶�t��ʱ��BD=t��OC=t��
��OD=8��t��
��DE=OE+OD=10��t��
��S=![]() DEOC=
DEOC=![]() ��10��t��t=��
��10��t��t=��![]() t2+5t��
t2+5t��
��S=��![]() t2+5t=��
t2+5t=��![]() ��t��5��2+
��t��5��2+![]() ��
��
����t=5ʱ��S���=![]() ��
��
��3���ɣ�2��֪����t=5ʱ��S���=![]() ��
��
����t=5ʱ��OC=5��OD=3��
��C��0��5����D��3��0����
�ɹ��ɶ����ã�CD=![]() ��
��
��ֱ��CD�Ľ���ʽΪ��y=kx+b��
��C��0��5����D��3��0����������ʽ�ã�
k=��![]() ��b=5��
��b=5��
��ֱ��CD�Ľ���ʽΪ��y=��![]() x+5��
x+5��
��E����EF��CD�������������P����ͼ1��
��ֱ��EF�Ľ���ʽΪ��y=��![]() x+b��
x+b��
��E����2��0������ã�b=��![]() ��
��
��ֱ��EF�Ľ���ʽΪ��y=��![]() x��
x��![]() ��
��
��y=��![]() x��
x��![]() ����y=��
����y=��![]() x2+3x+8�����ɷ�����ã�
x2+3x+8�����ɷ�����ã�
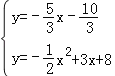 ��
��
��ã�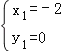 ��
��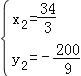 ��
��
��P��![]() ����
����![]() ����
����
����E��EG��CD������ΪG��
����t=5ʱ��S��ECD=![]() =
=![]() ��
��
��EG=![]() ��
��
����D��DN��CD������ΪN����ʹDN=![]() ������N��NM��x�ᣬ����ΪM����ͼ2��
������N��NM��x�ᣬ����ΪM����ͼ2��
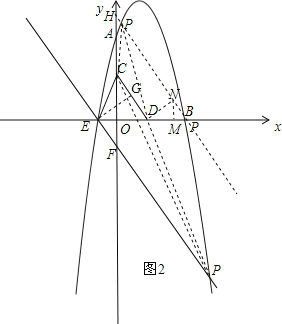
�ɵ���EGD�ס�DMN��
��![]() ��
��
����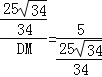 ��
��
��ã�DM=![]() ��
��
��OM=![]() ��
��
�ɹ��ɶ����ã�MN=![]() =
=![]() ��
��
��N��![]() ��
��![]() ����
����
����N��NH��CD���������߽����P����ͼ2��
��ֱ��NH�Ľ���ʽΪ��y=��![]() x+b��
x+b��
��N��![]() ��
��![]() ����������ʽ�ã�b=
����������ʽ�ã�b=![]() ��
��
��ֱ��NH�Ľ���ʽΪ��y=��![]() x+
x+![]() ��
��
��y=��![]() x+
x+![]() ����y=��
����y=��![]() x2+3x+8�����ɷ�����ã�
x2+3x+8�����ɷ�����ã�
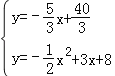 ��
��
��ã�![]() ��
��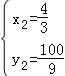 ��
��
��P��8��0����P��![]() ��
��![]() ����
����
��������������CED��������ʱ�����������ϴ��ڵ�P����E���⣩��ʹ��PCD�����������CED������������P������Ϊ��P��![]() ����
����![]() ����P��8��0����P��
����P��8��0����P��![]() ��
��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���ڴ������ĸ���ȫ��ͬ��С�����Ƿֱ���Ϊ1��2��3��4��С����Сǿ��ȡ����ȡ�����ֱ��ǣ�
С���������ȡһ��С����±�ţ�Ȼ��Żأ��������ȡһ��С���±�ţ�
Сǿ�������ȡһ��С����±�ţ����Żأ��������ȡһ��С���±�ţ�
��1���û���״ͼ�����б������ֱ��ʾС����Сǿ��������п��ܳ��ֵĽ����
��2���ֱ����С����Сǿ��������ı��֮�͵���5�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ�ƻ�����һЩ�ľ���ѧ����Ϊ��ѧУ����Χ�ơ��ڱʴ���Բ�桢ֱ�ߡ��ֱ������ľ��У�������Ҫ���ľ���ʲô������ѡ��ֻѡһ�֣��������⣬��ȫУ��Χ�������ȡ����ѧ�������ʾ����飬����������������Ƴ���ͼ��ʾ�IJ�������ͳ��ͼ���������������Ϣ�ش��������⣺
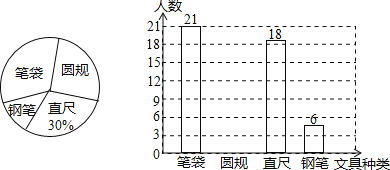
��1������ε����У�����ҪԲ���ѧ���ж�����������ȫ����ͳ��ͼ��
��2�����ȫУ��970��ѧ�����������ȫУѧ��������Ҫ�ֱʵ�ѧ���ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ͼ���ϵ���������P��Q���������ij�ֱ任�õ���ͼ���ϵĶ�Ӧ��P�䣬Q�䣬����PQ=P��Q�䣬���ǰ����ֱ任��Ϊ���Ⱦ�任�������б任�в�һ���ǵȾ�任���ǣ� ��
A��ƽ�� B����ת C����Գ� D��λ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����dz�ABC��BDE����ͼ��ʾ����ƴ��һ������A��B��D������ͬһֱ���ϣ�BMΪ��CBE��ƽ���ߣ�BNΪ��DBE��ƽ���ߣ�����MBN�Ķ����ǣ� ��
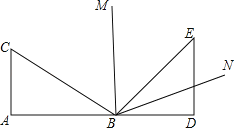
A��60�� B��67.5�� C��75�� D��85��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʹ����ֱ��������ȫ�ȵ������ǣ�������
A. һ����Ƕ�Ӧ��� B. ������Ƕ�Ӧ���
C. һ���߶�Ӧ��� D. б��һ��ֱ�DZ߶�Ӧ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=90����OA=9cm��OB=3cm��һ�������ڵ�B������һ��С��ӵ�A��������AO�������ٹ����O�������������ӵ�B��������BC��������ǰ������С��ǡ���ڵ�C����ס��С�����С��������ٶ�����������ߵ��ٶ���ȣ���ô���������ߵ�·��BC�Ƕ��٣�
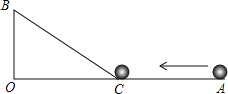
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����н�����ȷ���ǣ� ��
A��0������Ҳ��������
B������֮��Ϊ����������ͬΪ��
C����������ˣ����ķ����ɸ������ĸ�������
D����Ϊ�෴�����������ľ���ֵ��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P��0��m����y��ĸ������ϣ����M����m����m+1���ڣ� ��
A����һ���� B���ڶ����� C���������� D����������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com