
【题目】已知:二次函数y=mx2﹣(m+1)x+1.
(1)求证:该抛物线与x轴总有交点;
(2)若m为整数,当一元二次方程mx2﹣(m+1)x+1=0的根都是整数时,求m的值.
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,线段AB=10,动点P从点A出发,以每秒1个单位的速度,沿线段AB向终点B运动,同时,另一个动点Q从点B出发,以每秒3个单位的速度在线段AB上来回运动(从点B向点A运动,到达点A后,立即原速返回,再次到达B点后立即调头向点A运动.) 当点P到达B点时,P,Q两点都停止运动.设点P的运动时间为x.
![]()
(1)当x=3时,线段PQ的长为 .
(2)当P,Q两点第一次重合时,求线段BQ的长.
(3)是否存在某一时刻,使点Q恰好落在线段AP的中点上?若存在,请求出所有满足条件的x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形的两边长分别为5cm和10 cm,则此三角形的周长是( )
A. 15 cm B. 20 cm C. 25 cm D. 20 cm或25 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家莫伦在1925年发现了世界上第一个完美长方形.如图是一个完美长方形,它恰能被分割成10个大小不同的正方形,其中标注番号1的正方形边长为5,则这个完美长方形的面积为 .
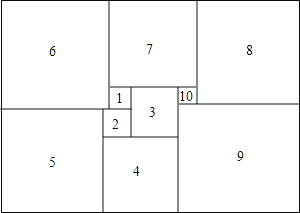
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,时钟的时针,分针均按时正常转动.
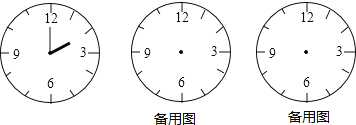
(1)分针每分针转动了 度,时针每分钟转动了 度;
(2)若现在时间恰好是2点整,求:
①经过多少分钟后,时针与分针第一次成90°角;
②从2点到4点(不含2点)有几次时针与分针成60°角,分别是几时几分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为E、F、Q为斜边AB的中点.
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系是 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
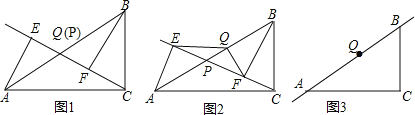
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com