
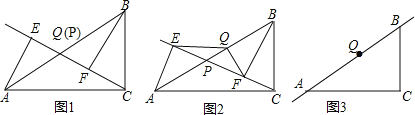
����Ŀ����֪����P��Rt��ABCб��AB��һ���㣨����A��B�غϣ����ֱ��A��B��ֱ��CP�����ߣ�����ֱ�ΪE��F��QΪб��AB���е㣮
��1����ͼ1������P���Q�غ�ʱ��AE��BF��λ�ù�ϵ�� ��QE��QF��������ϵ�� ��
��2����ͼ2������P���߶�AB�ϲ����Q�غ�ʱ�����ж�QE��QF��������ϵ��������֤����
��3����ͼ3������P���߶�BA����AB�����ӳ�����ʱ����ʱ��2���еĽ����Ƿ�������뻭��ͼ�β�����֤����
���𰸡���1��AE��BF��QE=QF����2��QE=QF����������3��QE=QF��������
��������
�����������1������AAS�Ƴ���AEQ�ա�BFQ���Ƴ�AE=BF���ɣ�
��2���ӳ�EQ��BF��D�������AEQ�ա�BDQ������ȫ�������ε����ʵó�EQ=QD������ֱ��������б�����е����ʵó����ɣ�
��3���ӳ�EQ��FB��D�������AEQ�ա�BDQ������ȫ�������ε����ʵó�EQ=QD������ֱ��������б�����е����ʵó����ɣ�
�⣺��1����ͼ1��
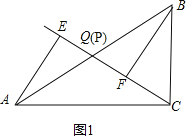
����P���Q�غ�ʱ��AE��BF��λ�ù�ϵ��AE��BF��QE��QF��������ϵ��AE=BF��
�����ǣ���QΪAB���е㣬
��AQ=BQ��
��AE��CQ��BF��CQ��
��AE��BF����AEQ=��BFQ=90����
����AEQ����BFQ��
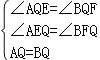
���AEQ�ա�BFQ��
��QE=QF��
�ʴ�Ϊ��AE��BF��QE=QF��
��2��
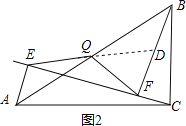
QE=QF��
֤�����ӳ�EQ��BF��D��
���ɣ�1��֪��AE��BF��
���AEQ=��BDQ��
����AEQ����BDQ��
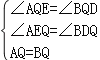
���AEQ�ա�BDQ��
��EQ=DQ��
�ߡ�BFE=90����
��QE=QF��
��3������P���߶�BA����AB�����ӳ�����ʱ����ʱ��2���еĽ��۳�����
֤�����ӳ�EQ��FB��D����ͼ3��
���ɣ�1��֪��AE��BF��
���AEQ=��BDQ��
����AEQ����BDQ��
���AEQ�ա�BDQ��
��EQ=DQ��
�ߡ�BFE=90����
��QE=QF��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����κ���y=mx2����m+1��x+1��
��1����֤������������x�����н��㣻
��2����mΪ��������һԪ���η���mx2����m+1��x+1=0�ĸ���������ʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����dz�ABC��BDE����ͼ��ʾ����ƴ��һ������A��B��D������ͬһֱ���ϣ�BMΪ��CBE��ƽ���ߣ�BNΪ��DBE��ƽ���ߣ�����MBN�Ķ����ǣ� ��
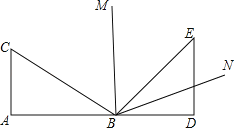
A��60�� B��67.5�� C��75�� D��85��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=90����OA=9cm��OB=3cm��һ�������ڵ�B������һ��С��ӵ�A��������AO�������ٹ����O�������������ӵ�B��������BC��������ǰ������С��ǡ���ڵ�C����ס��С�����С��������ٶ�����������ߵ��ٶ���ȣ���ô���������ߵ�·��BC�Ƕ��٣�
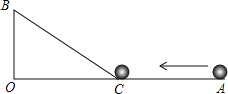
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2015�꣬�������˾ӻ���ίͨ����2014�������д���PM2.5��Դ�о��ɹ���������ʾ��Ҫ��Դ�У�A��������β����B����ҵVOCת����������ҵ���̣�C���ﳾ��D��Զ��E���糧��F��������ij��ѧѧϰС�������Щ���ݻ��Ƴ������������в�������ͳ��ͼ��ͼ1��ͼ2����
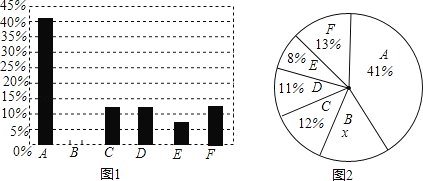
�������ͳ��ͼ�����ṩ����Ϣ����������⣺
��1��ͼ2������ͳ��ͼ�У�x��ֵ�� ��
��2���벹ȫͼ1�е�����ͳ��ͼ��
��3��ͼ2������ͳ��ͼ�У���A��������β�����������ε�Բ�ĽǶ���Ϊ �ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����н�����ȷ���ǣ� ��
A��0������Ҳ��������
B������֮��Ϊ����������ͬΪ��
C����������ˣ����ķ����ɸ������ĸ�������
D����Ϊ�෴�����������ľ���ֵ��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O��OAƽ����EOC��

��1������EOC=70��������BOD�Ķ�����
��2������EOC����EOD=2��3������BOD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y1=ax2+bx+c��a��0��ͼ���һ���֣������ߵĶ�������A��1��3������x���һ������B��4��0����ֱ��y2=mx+n��m��0���������߽���A��B���㣬���н��ۣ�
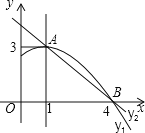
��2a+b=0��
��abc��0��
�۷���ax2+bx+c=3��������ȵ�ʵ������
����������x�����һ�������ǣ���1��0����
�ݵ�1��x��4ʱ����y2��y1��
������ȷ���ǣ� ��
A���٢ڢ� B���٢ۢ� C���٢ۢ� D���ڢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����6��8������ͼ�У�ÿ��С�����α߳���Ϊ1����O����ABC�Ķ����ΪС�����εĶ��㣮
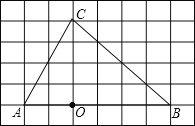
��1����OΪλ�����ģ�������ͼ������A��B��C����ʹ��A��B��C������ABCλ�ƣ���λ�Ʊ�Ϊ1��2��
��2�����ӣ�1���е�AA�䣬���ı���AA��C��C���ܳ���������������ţ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com