
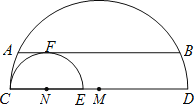
【题目】如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设![]() 、
、![]() 的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
【答案】8π.
【解析】
试题分析:过M作MG⊥AB于G,连MB,NF,根据垂径定理得到BG=AG=2,利用勾股定理可得MB2﹣MG2=22=4,再根据切线的性质有NF⊥AB,而AB∥CD,得到MG=NF,设⊙M,⊙N的半径分别为R,r,则z(x+y)=(CD﹣CE)(πR+πr)=(R2﹣r2)2π,即可得到z(x+y)的值.
解:过M作MG⊥AB于G,连MB,NF,如图,
而AB=4,
∴BG=AG=2,
∴MB2﹣MG2=22=4,
又∵大半圆M的弦与小半圆N相切于点F,
∴NF⊥AB,
∵AB∥CD,
∴MG=NF,
设⊙M,⊙N的半径分别为R,r,
∴z(x+y)=(CD﹣CE)(πR+πr),
=(2R﹣2r)(R+r)π,
=(R2﹣r2)2π,
=42π,
=8π.
故答案为:8π.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正方形的边长为a,以各边才为直径在正方形内画半圆,所围成的图形(图中阴影部分)的面积为( )
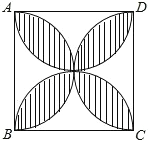
A.![]() a2﹣
a2﹣![]() B.
B.![]() ﹣a2 C.a2﹣
﹣a2 C.a2﹣![]() D.πa2﹣a2
D.πa2﹣a2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°.以AB长为一边作△ABD,且AD=BD,∠ADB=90°,取AB中点E,连DE、CE、CD.则∠EDC= °.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距900千米,一列快车从甲地出发匀速开往乙地,速度为120千米/时;快车开出30分钟时,一列慢车从乙地出发匀速开往甲地,速度为90千米/时.设慢车行驶的时间为x小时,快车到达乙地后停止行驶,根据题意解答下列问题:
(1)当快车与慢车相遇时,求慢车行驶的时间;
(2)请从下列(A),(B)两题中任选一题作答.
我选择: .
(A)当两车之间的距离为315千米时,求快车所行的路程;
(B)①在慢车从乙地开往甲地的过程中,求快慢两车之间的距离;(用含x的代数式表示)
②若第二列快车也从甲地出发匀速驶往乙地,速度与第一列快车相同,在第一列快车与慢车相遇后30分钟时,第二列快车与慢车相遇,直接写出第二列快车比第一列快车晚出发多少小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC边长为2,动点P从点A出发,以每秒1个单位长度的速度,沿A→B→C→A的方向运动,到达点A时停止.设运动时间为x秒,y=PC,则y关于x函数的图象大致为( )

A.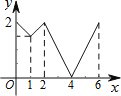 B.
B.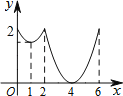
C.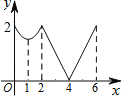 D.
D.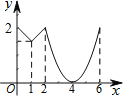
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是()
A. 有两组对边分别平行的四边形是平行四边形
B. 平行四边形的对角线互相平分
C. 平行四边形的对边平行且相等
D. 平行四边形的对角互补,邻角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=10,动点P从点A出发,以每秒1个单位的速度,沿线段AB向终点B运动,同时,另一个动点Q从点B出发,以每秒3个单位的速度在线段AB上来回运动(从点B向点A运动,到达点A后,立即原速返回,再次到达B点后立即调头向点A运动.) 当点P到达B点时,P,Q两点都停止运动.设点P的运动时间为x.
![]()
(1)当x=3时,线段PQ的长为 .
(2)当P,Q两点第一次重合时,求线段BQ的长.
(3)是否存在某一时刻,使点Q恰好落在线段AP的中点上?若存在,请求出所有满足条件的x的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com