
����Ŀ�������������900ǧ�ף�һ�п쳵�Ӽس������ٿ����ҵأ��ٶ�Ϊ120ǧ��/ʱ���쳵����30����ʱ��һ���������ҵس������ٿ����أ��ٶ�Ϊ90ǧ��/ʱ����������ʻ��ʱ��ΪxСʱ���쳵�����ҵغ�ֹͣ��ʻ�������������������⣺
��1�����쳵����������ʱ����������ʻ��ʱ�䣻
��2��������У�A������B����������ѡһ������
��ѡ�� ��
��A��������֮��ľ���Ϊ315ǧ��ʱ����쳵���е�·�̣�
��B�������������ҵؿ����صĹ����У����������֮��ľ��룻���ú�x�Ĵ���ʽ��ʾ��
�����ڶ��п쳵Ҳ�Ӽس�������ʻ���ҵأ��ٶ����һ�п쳵��ͬ���ڵ�һ�п쳵������������30����ʱ���ڶ��п쳵������������ֱ��д���ڶ��п쳵�ȵ�һ�п쳵����������Сʱ��
���𰸡���1�����쳵����������ʱ��������ʻ��4Сʱ����2��������
��������
�����������1����������ʻ��ʱ��ΪxСʱ����������ʱ���쳵��ʻ��·��+������ʻ��·��=900�������г����̣���⼴�ɣ�
��2����A��������֮��ľ���Ϊ315ǧ��ʱ�����������������������ǰ���315ǧ�ף��쳵��ʻ��·��+������ʻ��·��=900��315�����������������315ǧ�ף��쳵��ʻ��·��+������ʻ��·��=900+315���۵��쳵�����ҵ�ʱ���쳵��ʻ��7.5Сʱ��������ʻ��7Сʱ��7��90=630��315��������������ڣ�
��B���������������������쳵����ǰ��������쳵�����쳵�����ҵ�ʱ��
���ڵ�һ�п쳵������������30����ʱ��������ʻ��ʱ��Ϊ4+![]() =
=![]() Сʱ���쳵������ʻ��ʱ��Ϊ4+
Сʱ���쳵������ʻ��ʱ��Ϊ4+![]() +
+![]() =5Сʱ����ڶ��п쳵��ʻyСʱ��������������������ʱ���쳵��ʻ��·��+������ʻ��·��=900�����y��ֵ��������⼴�ɣ�
=5Сʱ����ڶ��п쳵��ʻyСʱ��������������������ʱ���쳵��ʻ��·��+������ʻ��·��=900�����y��ֵ��������⼴�ɣ�
�⣺��1����������ʻ��ʱ��ΪxСʱ���������
120��x+![]() ��+90x=900��
��+90x=900��
���x=4��
�𣺵��쳵����������ʱ��������ʻ��4Сʱ��
��2����A��������֮��ľ���Ϊ315ǧ��ʱ�������������
����������ǰ���315ǧ�ף���ʱ120��x+![]() ��+90x=900��315��
��+90x=900��315��
���x=2.5��
120��x+![]() ��=360��ǧ�ף���
��=360��ǧ�ף���
���������������315ǧ�ף���ʱ120��x+![]() ��+90x=900+315��
��+90x=900+315��
���x=5.5��
120��x+![]() ��=720��ǧ�ף���
��=720��ǧ�ף���
�۵��쳵�����ҵ�ʱ���쳵��ʻ��7.5Сʱ��������ʻ��7Сʱ��7��90=630��315��������������ڣ�
�𣺵�����֮��ľ���Ϊ315ǧ��ʱ���쳵���е�·��Ϊ360ǧ��720ǧ�ף�
��B���ٵ�������쳵����ǰ����0��x��4ʱ�������ľ���Ϊ900��120��x+![]() ����90x=840��210x��
����90x=840��210x��
��������쳵�����쳵�����ҵ�ǰ����4��x��7.5ʱ�������ľ���Ϊ120��x+![]() ��+90x��900=210x��840��
��+90x��900=210x��840��
���쳵�����ҵ�ʱ����7.5��x��10ʱ�������ľ���Ϊ90x��
���ڵ�һ�п쳵������������30����ʱ��������ʻ��ʱ��Ϊ4+![]() =
=![]() Сʱ���쳵������ʻ��ʱ��Ϊ4+
Сʱ���쳵������ʻ��ʱ��Ϊ4+![]() +
+![]() =5Сʱ��
=5Сʱ��
��ڶ��п쳵��ʻyСʱ�����������������⣬��
120y+![]() ��90=900��
��90=900��
���y=4![]() ��
��
5��4![]() =
=![]() ��Сʱ����
��Сʱ����
�𣺵ڶ��п쳵�ȵ�һ�п쳵������![]() Сʱ��
Сʱ��


 ���������ν�ϵ�д�
���������ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ�����������ĸ����ۣ�
��4ac��b2��0����4a+c��2b����3b+2c��0����m��am+b��+b��a��m�٩�1����
������ȷ���۵ĸ����ǣ� ��
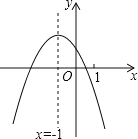
A��4�� B��3�� C��2�� D��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������A��B���㣬A��B����࣬��֪��B��Ӧ����Ϊ2����A��Ӧ����Ϊa��
��1����a=��3�����߶�AB�ij�Ϊ ��ֱ��д���������
��2������C���߶�AB֮�䣬��AC��BC=2�����C��ʾ�������ú�a��ʽ�ӱ�ʾ����
��3���ڣ�2���������£���D��������A�����һ�㣬��AC=2AD��BD=4BC����a��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
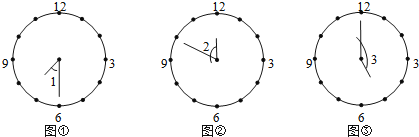
����Ŀ���������ָʱ�ӵ�ʱ����������ɵĽǣ���ͼ��ͼ�١�ͼ�ڡ�ͼ�����������ϵ�ʱ�̷ֱ��¼��ij��ѧ���糿�Ͽ�ʱ��7��30�������ѧʱ��11��50�������ѧʱ��17��00��
��1���ֱ�д��ͼ������ǵĶ�������1= �㡢��2= �㡢��3= �㣻
��2����ij�����㣬����ǿ��ܻ����90�㣬д�����ܵ�һ��ʱ��Ϊ ��
��3��������һԪһ�η��̵�֪ʶ������⣺�����ϣ���7��30��8��00֮�䣬����ǵ���90���ʱ���Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ε����߳��ֱ�Ϊ2��5���������ܳ�Ϊ��������
A. 9 B. 7 C. 12 D. 9��12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
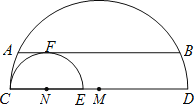
����Ŀ����ͼ��ֱ���ֱ�ΪCD��CE��������Բ�����ڵ�C�����ԲM������С��ԲN�����ڵ�F����AB��CD��AB=4����![]() ��
��![]() �ij��ֱ�Ϊx��y���߶�ED�ij�Ϊz����z��x+y����ֵΪ ��
�ij��ֱ�Ϊx��y���߶�ED�ij�Ϊz����z��x+y����ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AΪ��O��һ�㣬AB����O�ڵ�B��AO����O��C��CD��OB��E������O�ڵ�D������OD����AB=12��AC=8��
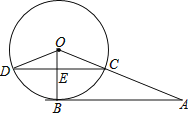
��1����OD�ij���
��2����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ����CD����O��һ���ң���CD��AB�ڵ�E��
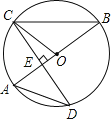
��1����֤����BCO=��D��
��2����CD=![]() ��AE=2������O�İ뾶��
��AE=2������O�İ뾶��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com