
【题目】如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
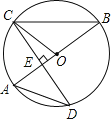
(1)求证:∠BCO=∠D;
(2)若CD=![]() ,AE=2,求⊙O的半径.
,AE=2,求⊙O的半径.
【答案】(1)见解析;(2)3
【解析】
试题分析:(1)由OB=OC,利用等边对等角得到一对角相等,再由同弧所对的圆周角相等得到一对角相等,等量代换即可得证;
(2)由弦CD与直径AB垂直,利用垂径定理得到E为CD的中点,求出CE的长,在直角三角形OCE中,设圆的半径OC=r,OE=OA﹣AE,表示出OE,利用勾股定理列出关于r的方程,求出方程的解即可得到圆的半径r的值.
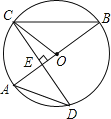
(1)证明:如图.
∵OC=OB,
∴∠BCO=∠B.
∵∠B=∠D,
∴∠BCO=∠D;
(2)解:∵AB是⊙O的直径,且CD⊥AB于点E,
∴CE=![]() CD=
CD=![]() ×4
×4![]() =2
=2![]() ,
,
在Rt△OCE中,OC2=CE2+OE2,
设⊙O的半径为r,则OC=r,OE=OA﹣AE=r﹣2,
∴r2=(2![]() )2+(r﹣2)2,
)2+(r﹣2)2,
解得:r=3,
∴⊙O的半径为3.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:初中数学 来源: 题型:
【题目】甲乙两地相距900千米,一列快车从甲地出发匀速开往乙地,速度为120千米/时;快车开出30分钟时,一列慢车从乙地出发匀速开往甲地,速度为90千米/时.设慢车行驶的时间为x小时,快车到达乙地后停止行驶,根据题意解答下列问题:
(1)当快车与慢车相遇时,求慢车行驶的时间;
(2)请从下列(A),(B)两题中任选一题作答.
我选择: .
(A)当两车之间的距离为315千米时,求快车所行的路程;
(B)①在慢车从乙地开往甲地的过程中,求快慢两车之间的距离;(用含x的代数式表示)
②若第二列快车也从甲地出发匀速驶往乙地,速度与第一列快车相同,在第一列快车与慢车相遇后30分钟时,第二列快车与慢车相遇,直接写出第二列快车比第一列快车晚出发多少小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形的两边长分别为5cm和10 cm,则此三角形的周长是( )
A. 15 cm B. 20 cm C. 25 cm D. 20 cm或25 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
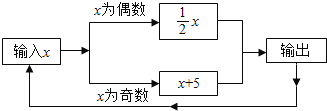
【题目】有一数值转换机,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是 ,依次继续下去…,第2015次输出的结果是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有若干除颜色外其他完全相同的小球,其中有6个黄球,将口袋中的球摇匀,从中任意摸出一个球记下颜色后再放回,通过大量重复上述实验后发现,摸到黄球的频率稳定在30%,由此估计口袋中共有小球 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣4x+3.
(1)把这个二次函数化成y=a(x﹣h)2+k的形式;
(2)写出二次函数的对称轴和顶点坐标;
(3)求二次函数与x轴的交点坐标;
(4)画出这个二次函数的图象;
(5)观察图象并写出y随x增大而减小时自变量x的取值范围.
(6)观察图象并写出当x为何值时,y>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com