
����Ŀ��ijũ��Ʒ���������罫�������ز�����ȫ�����������۵ĺ��Һͻ�����������Ʒ�������Ϣ���±���
��Ʒ | ���� | ���� |
��� | 1 kg/�� | 2 kg/�� |
���� | 10Ԫ/�� | 8Ԫ/�� |
�����ϱ��ṩ����Ϣ������������⣺
��1����֪�����ϰ��꣬�õ������ϱ����ĺ��Һͻ�����3000kg���������21000Ԫ�����ϰ���õ��������ֹ��ĺ��Һͻ��������ٴ���
��2������֮ǰ��������������ƽ����°��꣬�õ껹�������ϱ����ĺ��Һͻ�����2000kg�����У����ҵ�������������600kg����������°��꣬�����ϱ����ĺ���Ϊ![]() ��kg���������ϱ����ĺ��Һͻ�����õ�������Ϊ
��kg���������ϱ����ĺ��Һͻ�����õ�������Ϊ![]() ��Ԫ����д��
��Ԫ����д��![]() ��
��![]() ֮��ĺ�����ϵʽ�������°���õ��������ֹ��ĺ��Һͻ������ٻ�õ�������
֮��ĺ�����ϵʽ�������°���õ��������ֹ��ĺ��Һͻ������ٻ�õ�������
���𰸡���1�������ϰ���ũ��Ʒ���������ֹ��ĺ���1500���ͻ���750������2���°����ũ��Ʒ���������ֹ��ĺ��Һͻ������ٻ�õ�������Ϊ11600Ԫ��
��������
��1��������ϰ���ũ��Ʒ���������ֹ��ĺ���mkg������������Ϊ21000���������̼��ɣ�
��2������һ�κ���������һ�κ��������ʼ��ɽ������.
��1��������ϰ���ũ��Ʒ���������ֹ��ĺ���mkg��������3000-m��kg��
�����⣺10m+8��![]() ��21000��
��21000��
���m=1500��3000-m=1500��
�����ۺ�����1500������������![]() ��750������
��750������
�𣺽����ϰ���ũ��Ʒ���������ֹ��ĺ���1500���ͻ���750����
��2�������⣺W=10x+![]() =6x+8000��
=6x+8000��
��600��x��2000��
��x=600ʱ��y����Сֵ����СֵΪ11600Ԫ��
���°����ũ��Ʒ���������ֹ��ĺ��Һͻ������ٻ�õ�������Ϊ11600Ԫ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y = 2x2 -4x -6.
��1�����䷽����y = 2x2 -4x -6����y = a (x - h) 2 + k����ʽ����д���Գ���� �������ꡣ
��2����ƽ��ֱ������ϵ�У�����������κ�����ͼ��
��3����![]() ʱ����y��ȡֵ��Χ��
ʱ����y��ȡֵ��Χ��
��4������ͼ�����������ύ����Χ�ɵ������ε������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ű�����ȫ��ͬ��ֽ��![]() ��������ֱ����ĸ���ͬ�ļ���ͼ�Σ���������ֽ�Ʊ��泯��ϴ��.
��������ֱ����ĸ���ͬ�ļ���ͼ�Σ���������ֽ�Ʊ��泯��ϴ��.

��1�������������һ�ţ�������������ͼ�������ĶԳ�ͼ�εĸ��ʣ�
��2��С����С��Լ����һ����Ϸ�������Ϊ������С���������һ��ֽ�ƣ����Żأ�����С����ʣ�µ�ֽ�����������һ�ţ�����������������ͼ�ζ�����Գ�ͼ��С����ʤ������С����ʤ�������Ϸ��ƽ�������б���������״ͼ��˵�����ɣ�ֽ����![]() ��ʾ��.
��ʾ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
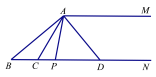
����Ŀ����ͼ������ABC�У�D��BC���е㣬DE��AB��E��DF��AC��F��BE=CF��
��1����֤��ADƽ�֡�BAC��
��2������EF����֤��AD��ֱƽ��EF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ABC��ƽ����BE���ACB��ǵ�ƽ����CE���ڵ�E��
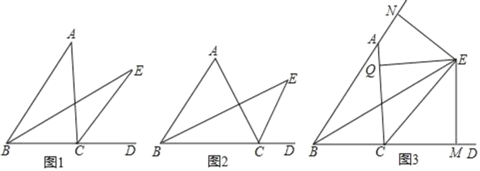
��1����ͼ1������BAC��40�㣬���BEC���� ����
��2����ͼ2������BAC��Ϊ60�㣬���BEC���� ���㣬д����BAC���BEC�Ĺ�ϵ����˵���������
��3����ͼ1�Ļ����Ϲ���E�ֱ���EN��BA��N��EQ��AC��Q��EM��BD��M����ͼ3��
��֤����ANE��AQE���������NAE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪![]() ��
��![]() ��
��![]() ����
����![]() ������
������![]() ��һ����(���
��һ����(���![]() ���غ�)��
���غ�)��![]() ��
��![]() �ֱ�ƽ��
�ֱ�ƽ��![]() ��
��![]() ��������
��������![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��
(1)��![]() �Ķ�����
�Ķ�����
(2)����![]() �˶�ʱ��
�˶�ʱ��![]() ��
��![]() ֮�����������������ϵ��˵�����ɣ�
֮�����������������ϵ��˵�����ɣ�
(3)����![]() �˶���ʹ
�˶���ʹ![]() ʱ,��
ʱ,��![]() �Ķ�����
�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������У�ÿ��С��Ķ��������㣮�����������α��ϵĵ�պ��ڸ���ϵĵ��Ϊ���㣮��ͼ��![]() �������ϵ����㹲��
�������ϵ����㹲��![]() ����
����![]() �������ϵ����㹲��
�������ϵ����㹲��![]() ��������۲�ͼ��������
��������۲�ͼ��������![]() �������ϵ�����ĸ��������˹��ɣ������������
�������ϵ�����ĸ��������˹��ɣ������������![]() �������ϵ����㹲��________����
�������ϵ����㹲��________����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+bx+c��x��ֱ��ڵ�A��B����y�ύ�ڵ�C����OA=1��OB=3������ΪD���Գ��ύx���ڵ�Q��

��1���������߶�Ӧ�Ķ��κ����ı���ʽ��
��2����P�������ߵĶԳ�����һ�㣬�Ե�PΪԲ�ĵ�Բ����A��B���㣬����ֱ��CD���У����P�����ꣻ
��3���������ߵĶԳ������Ƿ����һ��M��ʹ����DCM�ס�BQC��������ڣ������M�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���3x2��(a��3)x��a��0(a>0)��
(1)��֤������������������ȵ�ʵ������
(2)��������һ��������2����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com