
【题目】已知二次函数y = 2x2 -4x -6.
(1)用配方法将y = 2x2 -4x -6化成y = a (x - h) 2 + k的形式;并写出对称轴和 顶点坐标。
(2)在平面直角坐标系中,画出这个二次函数的图象;
(3)当![]() 时,求y的取值范围;
时,求y的取值范围;
(4)求函数图像与两坐标轴交点所围成的三角形的面积。

【答案】(1)![]() 对称轴是直线x=1, 顶点坐标是(1,-8);(2)图象见解析;(3
对称轴是直线x=1, 顶点坐标是(1,-8);(2)图象见解析;(3![]() );(4)12.
);(4)12.
【解析】
(1)先提取公因式2,然后再利用配方法将原式变形为y=2(x-1)2-8,最后再求得抛物线的对称和顶点坐标即可;
(2)根据二次函数画图即可;
(3)当x=1时,y有最小值,当x=4时,y有最大值,从而可求得y的范围;
(4)先求得抛物线与x轴、y轴的交点坐标,最后依据三角形的面积公式求解即可.
(1)y=2x2-4x-6
=2(x2-2x+1)-2-6
=2(x-1)2-8;
对称轴是直线x=1, 顶点坐标是(1,-8);
(2)令x=0,得y=-6,
令y=0,得2x2-4x-6=0,解得x=-1或x=3,
则抛物线与x轴的交点为:(-1,0),(3,0);与y轴的交点为:(0,-6).
由(1)题得:对称轴为x=1,顶点坐标为(1,-8),开口向上,故图象为: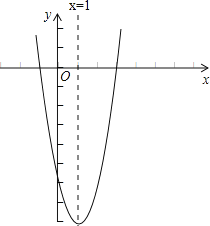
(3)当x=1时,y有最小值,最小值为-8,
∵![]() ,
,
∴y的最小值为10,
∴y的取值范围![]() .
.
(4)当x=0时,y=-6;
当y=0时,2x2-4x-6=0,解得:x=3或x=-1,
函数图像与两坐标轴交点所围成的三角形的面积=![]() .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
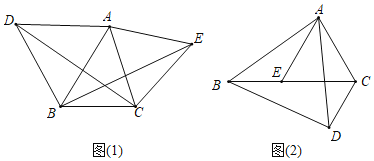
【题目】(1)感知:如图(1),在△ABC中,分别以AB、AC为边在△ABC外部作等边三角形△ABD、△ACE,连接CD、BE.求证:BE=DC;
(2)应用:如图(2),在△ABC中,AB>AC,分别以AB、AC为边在△ABC内部作等腰三角形△ABD、△ACE,点E恰好在BC边上,使AB=AD,AC=AE,且∠BAD=∠CAE,连接CD,CE=3cm,CD=2cm,△ABC的面积为25cm2,求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,∠BAC是△ABC的好角.
小丽展示了确定∠BAC是△ABC的好角的两种情形.情形一:如图2,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;情形二:如图3,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合.
探究发现
△ABC中,∠B=2∠C,经过两次折叠,∠BAC是不是△ABC的好角? (填“是”或“不是”).
小丽经过三次折叠发现了∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 .
根据以上内容猜想:若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 .
应用提升
(3)小丽找到一个三角形,三个角分别为15°、60°、105°,发现60°和105°的两个角都是此三角形的好角.
请你完成,如果一个三角形的最小角是4°,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤![]() PD=EC.其中有正确有( )个.
PD=EC.其中有正确有( )个.

A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(4,0),点B(0,6),点P是直线AB上的一个动点,已知点P的坐标为(m,n).
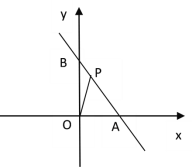
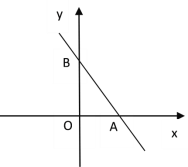
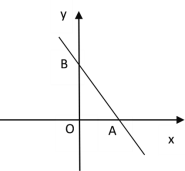
(1)当点P在线段AB上时(不与点A、B重合)
①当m=2,n=3时,求△POA的面积.
②记△POB的面积为S,求S关于m的函数解析式,并写出定义域.
(2)如果S△BOP:S△POA=1:2,请直接写出直线OP的函数解析式.(本小题只要写出结果,不需要写出解题过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为2,AD是BC边上的中线,M是AD上的动点,E是边AC的中点,则EM+CM的最小值为( )
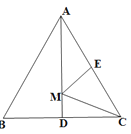
A.1B.12 C.3 D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农产品店利用网络将优质土特产销往全国,其中销售的核桃和花生这两种商品的相关信息如下表:
商品 | 核桃 | 花生 |
规格 | 1 kg/袋 | 2 kg/袋 |
利润 | 10元/袋 | 8元/袋 |
根据上表提供的信息,解答下列问题:
(1)已知今年上半年,该店销售上表规格的核桃和花生共3000kg,获得利润21000元,求上半年该店销售这种规格的核桃和花生各多少袋;
(2)根据之前的销售情况,估计今年下半年,该店还能销售上表规格的核桃和花生共2000kg,其中,核桃的销售量不低于600kg.假设今年下半年,销售上表规格的核桃为![]() (kg),销售上表规格的核桃和花生获得的总利润为
(kg),销售上表规格的核桃和花生获得的总利润为![]() (元),写出
(元),写出![]() 与
与![]() 之间的函数关系式,并求下半年该店销售这种规格的核桃和花生至少获得的总利润.
之间的函数关系式,并求下半年该店销售这种规格的核桃和花生至少获得的总利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com