解:(1)(-2xy
3z
2)
4=(-2)
4•x
4•(y
3)
4•(z
2)
4=16x
4y
12z
8;
(2)(xy+4)(xy-4)
=(xy)
2-4
2
=x
2y
2-16;
(3)(2x-3)(x-1)
=2x
2-2x-3x+3
=2x
2-5x+3;
(4)(54x
2y-108xy
2-36xy)÷(18xy)
=54x
2y÷18xy-108xy
2÷18xy-36xy÷18xy
=3x-6y-2;
(5)

a
2bc
3•(-2a
2b
2c)
2
=

a
2bc
3•4a
4b
4c
2
=2a
6b
5c
5;
(6)(x+y)
2-(x-y)
2
=[(x+y)+(x-y)][(x+y)-(x-y)]
=(x+y+x-y)(x+y-x+y)
=2x•2y
=4xy.
分析:(1)把括号中每一项四次方后,将结果相乘,利用幂的乘方法则:底数不变,只把指数相乘计算后,可得出最后结果;
(2)原式符合平方差公式的特点,故利用平方差公式化简,再利用积的乘方法则计算,即可得到结果;
(3)利用多项式乘以多项式的法则计算后,合并同类项即可得到结果;
(4)利用多项式除以单项式的法则:由多项式的每一项都除以单项式,并把所得的结果相加,再利用单项式除以多项式的法则计算,即可得到最后结果;
(5)根据运算顺序先算乘方运算,利用积的乘方运算法则:给积中每一个因式分别乘方,并把结果相乘计算后,再利用同底数幂的乘法法则计算,即可得到结果;
(6)利用平方差公式分解因式,去括号合并后,即可得到结果.
点评:此题考查了整式的混合运算,涉及的运算有:同底数幂的乘法、除法运算,积的乘方运算,多项式乘以多项式,多项式除以单项式运算,以及平方差公式的运用,熟练掌握运算法则是解本题的关键.

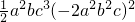
 a2bc3•(-2a2b2c)2
a2bc3•(-2a2b2c)2 a2bc3•4a4b4c2
a2bc3•4a4b4c2
