
【题目】如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.
(1)求tan∠DBC的值;
(2)求证:四边形OBEC是矩形.

【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)由四边形ABCD是菱形,得到对边平行,且BD为角平分线,利用两直线平行得到一对同旁内角互补,根据已知角之比求出相应度数,进而求出∠BDC度数,即可求出tan∠DBC的值;
(2)由四边形ABCD是菱形,得到对角线互相垂直,利用两组对边平行的四边形是平行四边形,再利用有一个角为直角的平行四边形是矩形即可得证.
试题解析:(1)解:∵四边形ABCD是菱形,∴AD∥BC,∠DBC=![]() ∠ABC,∴∠ABC+∠BAD=180°,∵∠ABC:∠BAD=1:2,∴∠ABC=60°,∴∠BDC=
∠ABC,∴∠ABC+∠BAD=180°,∵∠ABC:∠BAD=1:2,∴∠ABC=60°,∴∠BDC=![]() ∠ABC=30°,则tan∠DBC=tan30°=
∠ABC=30°,则tan∠DBC=tan30°=![]() ;
;
(2)证明:∵四边形ABCD是菱形,∴AC⊥BD,即∠BOC=90°,∵BE∥AC,CE∥BD,∴BE∥OC,CE∥OB,∴四边形OBEC是平行四边形,则四边形OBEC是矩形.


科目:初中数学 来源: 题型:
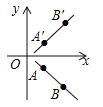
【题目】王杰同学在解决问题“已知A、B两点的坐标为A(3,﹣2)、B(6,﹣5)求直线AB关于x轴的对称直线A′B′的解析式”时,解法如下:先是建立平面直角坐标系(如图),标出A、B两点,并利用轴对称性质求出A′、B′的坐标分别为A′(3,2),B′(6,5);然后设直线A′B′的解析式为y=kx+b(k≠0),并将A′(3,2)、B′(6,5)代入y=kx+b中,得方程组:![]() ,解得
,解得![]() ,最后求得直线A′B′的解析式为y=x﹣1.则在解题过程中他运用到的数学思想是( )
,最后求得直线A′B′的解析式为y=x﹣1.则在解题过程中他运用到的数学思想是( )
A.分类讨论与转化思想 B.分类讨论与方程思想
C.数形结合与整体思想 D.数形结合与方程思想
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,如果AB=DC,当AB________DC时,四边形ABCD是平行四边形;当AD________BC时,四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某油箱容量为60 L的汽车,加满汽油后行驶了100 Km时,油箱中的汽油大约消耗了![]() ,如果加满汽油后汽车行驶的路程为x Km,邮箱中剩油量为y L,则y与x之间的函数解析式和自变量取值范围分别是( )
,如果加满汽油后汽车行驶的路程为x Km,邮箱中剩油量为y L,则y与x之间的函数解析式和自变量取值范围分别是( )
A.y=0.12x,x>0 B.y=60﹣0.12x,x>0 C.y=0.12x,0≤x≤500 D.y=60﹣0.12x,0≤x≤500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=3x2向左平移2个单位,再向下平移1个单位,所得抛物线为( )
A.y=3(x﹣2)2﹣1
B.y=3(x﹣2)2+1
C.y=3(x+2)2﹣1
D.y=3(x+2)2+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com