
分析 根据两直线相交的问题,把(-1,m)分别代入y1=ax+1和y2=-2ax+4可解得a=-1,m=-2,则A(-1,-2),再确定直线y1与x轴的交点C(1,0),直线y2与x轴的交点B(-2,0),设P点坐标为(t,-t+1),分类讨论:当t<-1时,利用S△ABP=S△PBC-S△ABC得$\frac{1}{2}$(1+2)×(-t+1)-3=6,解得t=-5,此时P点坐标为(-5,4);当t>1时,利用S△ABP=S△PBC+S△ABC得$\frac{1}{2}$(1+2)×|-t+1|+3=6,解得t=3,此时P点坐标为(3,-2).
解答 解:把(-1,m)分别代入y1=ax+1和y2=-2ax+4得-a+1=m,2a+4=m,解得a=-1,m=-2,则A(-1,-2),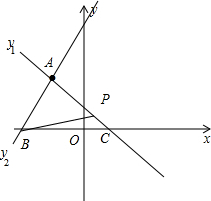 两直线解析式分别为y1=-x+1,y2=2x+4,
两直线解析式分别为y1=-x+1,y2=2x+4,
直线y1与x轴的交点C(1,0),直线y2与x轴的交点B(-2,0),
设P点坐标为(t,-t+1),
S△ABC=$\frac{1}{2}$×(1+2)×2=3,
当t<-1时,S△ABP=S△PBC-S△ABC,即$\frac{1}{2}$(1+2)×(-t+1)-3=6,解得t=-5,此时P点坐标为(-5,4);
当t>1时,S△ABP=S△PBC+S△ABC,即$\frac{1}{2}$(1+2)×|-t+1|+3=6,解得t=3,此时P点坐标为(3,-2);
综上所述,点P的坐标为(-5,4)或(3,-2).
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
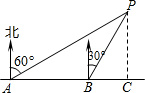 如图,小明同学在东西走向的山阴路A处,测得一处公共自行车租用服务点P在北偏东60°方向上,在A处往东200米的B处,又测得该服务点P在北偏东30°方向上,则该服务点P到山阴路的距离PC为100$\sqrt{3}$米.
如图,小明同学在东西走向的山阴路A处,测得一处公共自行车租用服务点P在北偏东60°方向上,在A处往东200米的B处,又测得该服务点P在北偏东30°方向上,则该服务点P到山阴路的距离PC为100$\sqrt{3}$米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
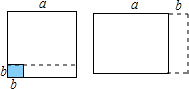 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )
如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )| A. | (a+2b)(a-b)=a2+ab-2b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | a2-b2=(a+b)(a-b) | D. | (a-b)2=a2-2ab-b2. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
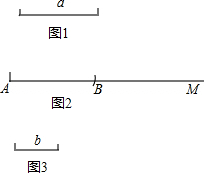 阅读材料:用尺规作图要求作线段AB等于线段a时,小明的具体作法如下:
阅读材料:用尺规作图要求作线段AB等于线段a时,小明的具体作法如下:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com