
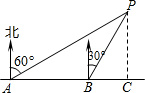
 如图,小明同学在东西走向的山阴路A处,测得一处公共自行车租用服务点P在北偏东60°方向上,在A处往东200米的B处,又测得该服务点P在北偏东30°方向上,则该服务点P到山阴路的距离PC为100$\sqrt{3}$米.
如图,小明同学在东西走向的山阴路A处,测得一处公共自行车租用服务点P在北偏东60°方向上,在A处往东200米的B处,又测得该服务点P在北偏东30°方向上,则该服务点P到山阴路的距离PC为100$\sqrt{3}$米. 分析 分别在两个直角三角形中由锐角三角函数的定义用PC分别表示出AC、BC,利用两线段的差等于200米列出关于线段PC的式子,求得PC即可.
解答 解:∵在Rt△PBC中,$\frac{PC}{BC}$=tan∠PBC,
∴BC=$\frac{PC}{tan60°}$=$\frac{\sqrt{3}}{3}$PC,
∵在Rt△PAC中,$\frac{PC}{AC}$=tan∠PAC,
∴AC=$\frac{PC}{tan30°}$=$\sqrt{3}$PC,
∵AB=AC-BC=200,
∴$\sqrt{3}$PC-$\frac{\sqrt{3}}{3}$PC=200,
解得:PC=100$\sqrt{3}$.
故答案为100$\sqrt{3}$米.
点评 本题考查了解直角三角形的应用-方向角问题,解决此题的关键是弄清直角三角形的三边与其锐角的关系,进而列出有关的等式,解之即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 448×108 | B. | 44.8×109 | C. | 4.48×1010 | D. | 4×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≠1 | B. | x>-3且x≠1 | C. | x≥-3 | D. | x≥-3且x≠1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com