
分析 (1)在y=-$\frac{3}{4}$x+1中令y=0,解得x的值即可求得A的坐标;
把(-$\frac{8}{3}$,m)代入y=-$\frac{3}{4}$x+1,求得m的值即可求得B的坐标,然后利用待定系数法求得反比例函数的解析式;
(2)设直线y=-$\frac{3}{4}$x+1与y轴的交点是M.则M的坐标是(0,1).过B作AN⊥BM,并截取AN=4,作NE∥y轴,交AM于点E,利用△ANE∽△OAM,求得NE的长,则把把B上下平移EN个单位长度就是C的坐标.
解答 解:(1)在y=-$\frac{3}{4}$x+1中令y=0,解得x=$\frac{4}{3}$,
则A的坐标是($\frac{4}{3}$,0).
把B(-$\frac{8}{3}$,m)代入y=-$\frac{3}{4}$x+1,得m=2+1=3,
则B的坐标是(-$\frac{8}{3}$,3).
把(-$\frac{8}{3}$,3)代入y=$\frac{k}{x}$得k=-8,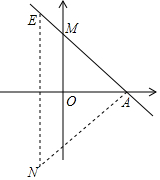
则反比例函数的解析式是y=-$\frac{8}{x}$;
(2)设直线y=-$\frac{3}{4}$x+1与y轴的交点是M.则M的坐标是(0,1).
过B作AN⊥BM,并截取AN=4,作NE∥y轴,交AM于点E.
在直角△OAM中,AM=$\sqrt{O{A}^{2}+O{M}^{2}}$=$\frac{5}{3}$.
∵NE∥OM,
∴∠NEA=∠AMO,
又∵∠AOM=∠EAN,
∴△ANE∽△OAM,
∴$\frac{EN}{AM}$=$\frac{AN}{OA}$,即$\frac{EN}{\frac{5}{3}}$=$\frac{4}{\frac{4}{3}}$,
解得:EN=5,即BC=5.
则把B上下平移5个单位长度就是C的坐标,则C的坐标是(-$\frac{8}{3}$,8)或(-$\frac{8}{3}$,-2).
点评 本题考查了待定系数法求函数的解析式以及相似三角形的判定与性质,正确求得BC的长度是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
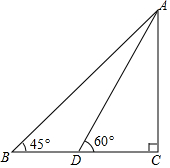 如图,某滑雪运动员训练时的斜坡示意图,某次训练拟将难度系数加大,决定将训练的斜坡的倾角由45°升为60°,已知原斜坡AB的长为3$\sqrt{6}$米,点B、D、C在同一水平地面上.若斜坡的正前方能有6米长的空地就能保证安全,已知原斜坡屈的前方有3米长的空地,进行这样的改造是否可行?并说明理由.(参考数据:$\sqrt{3}$=1.732,$\sqrt{6}$=2.449)
如图,某滑雪运动员训练时的斜坡示意图,某次训练拟将难度系数加大,决定将训练的斜坡的倾角由45°升为60°,已知原斜坡AB的长为3$\sqrt{6}$米,点B、D、C在同一水平地面上.若斜坡的正前方能有6米长的空地就能保证安全,已知原斜坡屈的前方有3米长的空地,进行这样的改造是否可行?并说明理由.(参考数据:$\sqrt{3}$=1.732,$\sqrt{6}$=2.449)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com