如图.在平面直角坐标系xOy中.已知点A(3.0).点B(0.3).点O为原点．动点C.D分别在直线AB.OB上.将△BCD沿着CD折叠.得△B'CD．(Ⅰ)如图1.若CD⊥AB.点B'恰好落在点A处.求此时点D的坐标,(Ⅱ)如图2.若BD=AC.点B'恰好落在y轴上.求此时点C的坐标,(Ⅲ)若点C的横坐标为2.点B'落在x轴上.求点B'的坐标．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

如图，在平面直角坐标系xOy中，已知点A（3，0），点B（0，3），点O为原点．动点C、D分别在直线AB、OB上，将△BCD沿着CD折叠，得△B'CD．

（Ⅰ）如图1，若CD⊥AB，点B'恰好落在点A处，求此时点D的坐标；

（Ⅱ）如图2，若BD=AC，点B'恰好落在y轴上，求此时点C的坐标；

（Ⅲ）若点C的横坐标为2，点B'落在x轴上，求点B'的坐标（直接写出结果即可）．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：江苏省盐城市东台市第二联盟2018-2019学年八年级上第一次月考数学试卷 题型：单选题

如图，△ACE≌△DBF，若∠E=∠F，AD=8，BC=2，则AB等于（　　）

A. 6 B. 5 C. 3 D. 不能确定

查看答案和解析>>

科目：初中数学 来源：上海市浦东新区第四教育署2018-2019学年七年级（五四学制）上学期期中考试数学试卷 题型：填空题

计算：_____________．

查看答案和解析>>

科目：初中数学 来源：四川省2019届九年级上学期半期考试数学试卷 题型：解答题

“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图）：将给定的锐角∠AOB置于直角坐标系中，边OB在x轴上、边OA与函数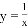的图象交于点P，以P为圆心、以2OP为半径作弧交图象于点R．分别过点P和R作x轴和y轴的平行线，两直线相交于点M，连接OM得到∠MOB，则∠MOB=∠AOB．要明白帕普斯的方法，请研究以下问题：

（1）设P（，）、R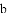（，），求直线OM对应的函数表达式（用含，的代数式表示）；

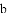
（2）分别过点P和R作y轴和x轴的平行线，两直线相交于点Q．请说明Q点在直线OM上，并据此证明∠MOB=∠AOB；

（3）应用上述方法得到的结论，你如何三等分一个钝角（用文字简要说明）

查看答案和解析>>

科目：初中数学 来源：四川省2019届九年级上学期半期考试数学试卷 题型：解答题

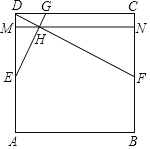
如图，在正方形ABCD中，点E，F分别是边AD，BC的中点，连接DF，过点E作EH⊥DF，垂足为H，EH的延长线交DC于点G．

（1）猜想DG与CF的数量关系，并证明你的结论；

（2）过点H作MN∥CD，分别交AD，BC于点M，N，若正方形ABCD的边长为10，点P是MN上一点，求△PDC周长的最小值．

查看答案和解析>>

科目：初中数学 来源：天津市河北区2018届中考二模数学试卷 题型：填空题

解不等式组

请结合题意填空，完成本题的解答．

（Ⅰ）解不等式①，得　　；

（Ⅱ）解不等式②，得　　；

（Ⅲ）把不等式①和②的解集在数轴上表示出来：

（Ⅳ）原不等式组的解集为　　．

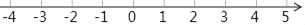
查看答案和解析>>

科目：初中数学 来源：天津市河北区2018届中考二模数学试卷 题型：单选题

如图，正方形ABCD的边长为4，点M是CD的中点,动点E从点B出发，沿BC运动，到点C时停止运动，速度为每秒1个长度单位；动点F从点M出发，沿M→D→A远动，速度也为每秒1个长度单位：动点G从点D出发，沿DA运动，速度为每秒2个长度单位，到点A后沿AD返回，返回时速度为每秒1个长度单位，三个点的运动同时开始，同时结束．设点E的运动时间为x，△EFG的面积为y，下列能表示y与x的函数关系的图象是（　　）