
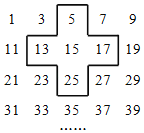
【题目】将连续的奇数1,3,5,7,9,…排成如图所示的数表.
(1)探索任意一个十字形框中的五个数之和与中间的数的关系是 .
(2)若十字框中的五数之和是2015,请求出此时框中的五个数分别是什么?
【答案】(1)五个数之和为中间数的5倍;(2)五个数分别为393,401,403,405,413.
【解析】
(1)设中间的数为x,表示出一个十字形框中的五个数之和,即可得到结果;
(2)根据(1)表示的五个数之和,求出x的值,即可确定出所求.
解:(1)设中间是数为x,其余数为x﹣10,x+10,x﹣2,x+2,
五个数之和为x﹣10+x+10+x﹣2+x+2+x=5x,
则任意一个十字形框中的五个数之和与中间的数的关系是:五个数之和为中间数的5倍;
故答案为:五个数之和为中间数的5倍;
(2)根据(1)得:5x=2015,
解得:x=403,
∴x﹣10=393,x+10=413,x﹣2=401,x+2=405,
则五个数分别为393,401,403,405,413.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】.如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD,其中正确的有( )

A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
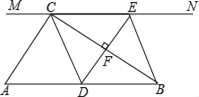
【题目】如图:在Rt△ABC中,∠ACB=90°,AB=6,过点C的直线MN∥AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连结CD,BE,
(1)当点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由
(2)在(1)的条件下,当∠A= 时四边形BECD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发商的经适房的三个居民小区A、B、C在同一条直线上,位置如图所示.其中小区B到小区A、C的距离分别是70m和150m,现在想在小区A、C之间建立一个超市,要求各小区居民到超市总路程的和最小,那么超市的位置应建在( )
![]()
A.小区AB.小区BC.小区CD.AC的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年6月6日,工信部正式向四家电信企业发放![]() 商用牌照,标志着
商用牌照,标志着![]() 元年开始华为公司作为
元年开始华为公司作为![]() 行业的领军者,已经具备从芯片、产品到系统组网的世界领先的
行业的领军者,已经具备从芯片、产品到系统组网的世界领先的![]() 技术,是全球唯一一家能够提供端到端
技术,是全球唯一一家能够提供端到端![]() 商用解决方案的通讯企业为了了解某中学生对
商用解决方案的通讯企业为了了解某中学生对![]() 通讯技术的了解情况,随机抽取部分学生进行问卷,将结果分成“非常了解”“比较了解”、“一般了解”、“不了解”四种类型,分别记为
通讯技术的了解情况,随机抽取部分学生进行问卷,将结果分成“非常了解”“比较了解”、“一般了解”、“不了解”四种类型,分别记为![]() ,根据调查结果给制了如下尚不完整的两个统计图
,根据调查结果给制了如下尚不完整的两个统计图
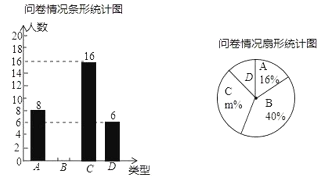
(1)本次问卷共随机调查了 名学生,在扇形统计图中![]() _ _,“
_ _,“![]() ”所在扇形的圆心角的度数为 度;
”所在扇形的圆心角的度数为 度;
(2)请根据数据信息补全条形统计图;
(3)若该校有![]() 名学生,估计选择“非常了解”、“比较了解”的学生共约有多少人?
名学生,估计选择“非常了解”、“比较了解”的学生共约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
普通间(元/人/天) | 豪华间(元/人/天) | 贵宾间(元/人/天) | |
三人间 | 50 | 100 | 500 |
双人间 | 70 | 150 | 800 |
单人间 | 100 | 200 | 1500 |
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了 人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com