
����Ŀ����ͼһ����֪������y��ax2+bx+c��ͼ����A��0��3����B��1��0������Գ���Ϊֱ��l��x��2������A��AC��x�ύ�������ڵ�C����AOB��ƽ���߽��߶�AC�ڵ�E����P���������ϵ�һ�����㣬���������Ϊm��
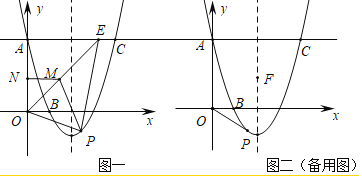
��1���������ߵĽ���ʽ��
��2��������P��ֱ��OE�·����������ϣ�����PE��PO����mΪ��ֵʱ���ı���AOPE��������������ֵ�����ı���AOPE������ʱ�����߶�OE��ȡ��M����y����ȡ��N����PM+MN+![]() ANȡ��Сֵʱ�������ʱN������꣮
ANȡ��Сֵʱ�������ʱN������꣮
��3����ͼ����F�������ߵĶԳ���l�ϵ�һ�㣬�����������Ƿ���ڵ�P��ʹ��POF��Ϊ�Ե�PΪֱ�Ƕ���ĵ���ֱ�������Σ������ڣ�ֱ��д�����з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y��x2��4x+3����2��N��0��![]() ������3�����ڣ����ɣ�������.
������3�����ڣ����ɣ�������.
��������
��1������������x�����һ������ΪD���ɶԳ��Եã�D��3��0�����������ߵĽ���ʽΪ��y=a��x-1����x-3������A��0��3������ã�3=3a��a=1��������⣻
��2������A����б��Ϊ45����ֱ��AH������P��PH��AH�ڵ�H����OE�ڵ�M����y���ڵ�N�����NΪ��������⣻
��3����P�ڶԳ������ߣ�����x���·���P�ڶԳ������ߣ�����x���Ϸ���P�ڶԳ�����ұߣ�����x���·���P�ڶԳ�����ұߣ�����x���Ϸ�����������ֱ���⼴�ɣ�
�⣺��1������������x�����һ������ΪD��
�ɶԳ��Եã�D��3��0����
�������ߵĽ���ʽΪ��y��a��x��1����x��3����
��A��0��3������ã�3��3a��a��1��
�������ߵĽ���ʽ��y��x2��4x+3��
��2����ͼ1���ߡ�AOE������Ƕ�ֵ�����Ե���OEP������ʱ���ı���AOPE������
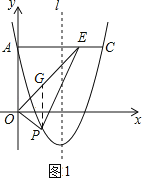
��P��m��m2��4m+3����
��OEƽ�֡�AOB����AOB��90�㣬���AOE��45�㣬���AOE�ǵ���ֱ�������Σ�
��AE��OA��3����E��3��3������OE�Ľ���ʽΪ��y��x��
��P��PG��y�ᣬ��OE�ڵ�G����G��m��m����
��PG��m����m2��4m+3������m2+5m��3��
��S�ı���AOPE��S��AOE+S��POE��![]() ��3��3+
��3��3+![]() PGAE��
PGAE��![]() +
+![]() ��3������m2+5m��3������
��3������m2+5m��3������![]() m2+
m2+![]() ��
��
�ߩ�![]() ��0��
��0��
�൱m��![]() ʱ��S�����ֵ����ʱ��P��
ʱ��S�����ֵ����ʱ��P��![]() ����
����![]() ����
����
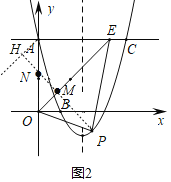
����A����б��Ϊ45���ֱ��AH������P��PH��AH�ڵ�H����OE�ڵ�M����y���ڵ�N�����NΪ����
��NH��![]() AN��
AN��
��ʱPM+MN+![]() AN��PM+MN+HN��PHΪ��Сֵ��
AN��PM+MN+HN��PHΪ��Сֵ��
��ֱ��PH�ı���ʽΪ��y����x+b������P�����������ʽ����ã�
ֱ��PH�ı���ʽΪ��y����x+![]() ��
��
�ʵ�N��0��![]() ����
����
��3�����ڣ����ɣ�
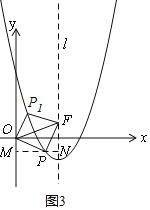
�ٵ�P�ڶԳ������ߣ�����x���·�ʱ����ͼ2����P��MN��y�ᣬ��y����M����l��N��
�ߡ�OPF�ǵ���ֱ�������Σ���OP��PF��
���OMP�ա�PNF��AAS����
��OM��PN��
��P��m��m2��4m+3������m2+4m��3��2��m��
��ã�m��![]() ����ȥ����
����ȥ����![]()
��P��������![]() ��
��![]() ����
����
�ڵ�P�ڶԳ������ߣ�����x���Ϸ�ʱ����ͼ3��
ͬ���ã�2��m��m2��4m+3����ã�m��![]() ��
��![]() ����ȥ����
����ȥ����
�ʵ�P��![]() ��
��![]() ����
����
�۵�P�ڶԳ�����ұߣ�����x���·�ʱ��
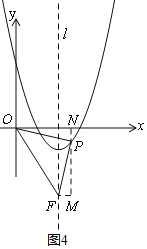
��ͼ3����P��MN��x����N����F��FM��MN��M��
ͬ���á�ONP�ա�PMF��
��PN��FM��
��m2+4m��3��m��2��
��ã�m��![]() ��
��![]() ����ȥ����
����ȥ����
P��������![]() ��
��![]() ����
����
�ܵ�P�ڶԳ�����ұߣ�����x���Ϸ�ʱ��
ͬ����m2��4m+3��m��2��
��ã�m��![]() ��
��![]() ����ȥ����
����ȥ����
��P����������![]() ��
��![]() ����
����
���ϣ���P������Ϊ����![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����


 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��Oֱ����ACΪ��O���ң�����O��ĵ�D��DE��OA�ڵ�E����AC�ڵ�F������DC���ӳ���AB���ӳ����ڵ�P������D=2��A����CH��AB�ڵ�H��
��1���ж�ֱ��DC����O��λ�ù�ϵ����˵�����ɣ�
��2����HB=2��cosD=![]() �������AC�ij���
�������AC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2-2(k-1)x+k2 =0������ʵ����x1.x2.
(1)��ʵ ��k��ȡֵ��Χ;
(2)��(x1+1)(x2+1)=2������k��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������![]() �У�����������
�У�����������![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ����
��ͼ����![]() ��
��

��![]() ���ֱ��������������ı���ʽ��
���ֱ��������������ı���ʽ��
��![]() ����ֱ��
����ֱ��![]() ����ƽ��
����ƽ��![]() ����λ���Ⱥ���
����λ���Ⱥ���![]() �ύ�ڵ�
�ύ�ڵ�![]() ���뷴��������ͼ���ڵ��������ڵĽ���Ϊ
���뷴��������ͼ���ڵ��������ڵĽ���Ϊ![]() ������
������![]() ��
��![]() �����
�����![]() �����꼰
�����꼰![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC����ABΪֱ���ġ�O��BC�ཻ�ڵ�D����CA���ӳ����ཻ�ڵ�E������D��DF��AC�ڵ�F��

��1��֤����DF�ǡ�O�����ߣ�
��2����AC��3AE��FC��6����AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
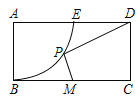
����Ŀ����ͼ������ABCD�У�AB=2��AD=4��M����BC���е㣬AΪԲ�ģ�ABΪ�뾶��Բ��AD�ڵ�E����P�ڻ�BE���˶�����PM+![]() DP����СֵΪ____________��
DP����СֵΪ____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����С��һ��Բ���ε���ˮ�ܵ�������ά����ԱΪ�����ܵ�����ȷ���ܵ�Բ�ν���İ뾶����ͼ��ˮƽ���õ����ѹܵ���ˮ���ֵĽ�����
(1)������ֱ�ߺ�Բ�����������ˮ�ܵ���Բ�ν����Բ��(������ͼ�ۼ�)��
(2)�������ˮ�ܵ���ˮ���ֵ�ˮ���AB��8 cm��ˮ������ط��ĸ߶�Ϊ2 cm�������Բ�ν���İ뾶��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ�������ε�ֱ�Ƕ���������ԭ�㣬��OAB=30�㣬����A�ڷ���������y=![]() ��x��0����ͼ���ϣ�����B�ķ�������������ʽΪ��������
��x��0����ͼ���ϣ�����B�ķ�������������ʽΪ��������

A. y=��![]() B. y=��
B. y=��![]() C. y=��
C. y=��![]() D. y=
D. y=![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com