
【题目】如图,![]() 中,
中,![]() 分别是
分别是![]() 的中点.
的中点.

![]() 求证:四边形
求证:四边形![]() 是菱形
是菱形
![]() 如果
如果![]() ,求四边形
,求四边形![]() 的面积.
的面积.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由平行四边形的性质可得BC=AD,BC∥AD,由中点的性质可得EC=AF,可证四边形AECF为平行四边形,由直角三角形的性质可得AE=EC,即可得结论;
(2)由勾股定理可求AC的长,可求S△ABC=![]() AB×AC=2
AB×AC=2![]() ,即可求四边形AECF的面积.
,即可求四边形AECF的面积.
证明:(1)∵在ABCD中,
∴BC=AD,BC∥AD,
又∵E,F分别是边BC,AD的中点,
∴EC=![]() BC,AF=
BC,AF=![]() AD,
AD,
∴EC=AF,且EC∥AF,
∴四边形AECF为平行四边形.
在Rt△ABC中,∠BAC=90°,E是BC边中点,
∴AE=EC,
∴四边形AECF是菱形;
(2)∵∠BAC=90°,AB=2,BC=4,
∴AC=![]() =2
=2![]() ,
,
∴S△ABC=![]() AB×AC=2
AB×AC=2![]() ,
,
∵点E是BC的中点,
∴S△AEC=![]() S△ABC=
S△ABC=![]() ,
,
∵四边形AECF是菱形
∴四边形AECF的面积=2S△AEC=2![]() .
.


科目:初中数学 来源: 题型:
【题目】某天,一蔬菜经营户用180元钱从蔬菜批发市场批了西红柿和豆角共40千克到菜市场去卖,西红柿和豆角这天的批发价与零售价如下表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/千克) | 3.6 | 4.6 |
零售价(单位:元/千克) | 5.4 | 7.5 |
问:他当天卖完这些西红柿和豆角能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“美化城市,改善人民居住环境”是城市建设的一项重要内容.北京市将重点围绕城市副中心、大兴国际机场、冬奥会、世园会、永定河、温榆河、南中轴等重要节点区域绿化,到2022年,全市将真正形成一片集“万亩城市森林、百万乔灌树木、百种乡土植物、二十四节气林窗、四季景观大道”于一体的城市森林.2018年当年计划新增造林23万亩,2019年计划新增造林面积大体相当于27.8个奥森公园的面积,预计2020年计划新增造林面积达到38.87万亩,求2018年至2020年计划新增造林面积的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,BC![]() 2,∠BAC
2,∠BAC![]() 30°,斜边AB的两个端点分别在相互垂直的射线OM,ON上滑动,下列结论: ①若C,O两点关于AB对称,则OA
30°,斜边AB的两个端点分别在相互垂直的射线OM,ON上滑动,下列结论: ①若C,O两点关于AB对称,则OA![]() ;②C,O两点距离的最大值为4;③若AB平分CO,则AB⊥CO;④斜边AB的中点D运动路径的长为
;②C,O两点距离的最大值为4;③若AB平分CO,则AB⊥CO;④斜边AB的中点D运动路径的长为![]() .
.
其中正确的是( )
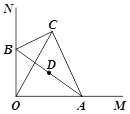
A. ①② B. ①②③ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点![]() 为原点,点
为原点,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,且
,且![]() 满足
满足![]()
(1)A、B两点对应的数分别为![]() _____,
_____,![]() ______;
______;
(2)若将数轴折叠,使得![]() 点与
点与![]() 点重合,则原点
点重合,则原点![]() 与数______表示的点重合.
与数______表示的点重合.
(3)若点A、B分别以4个单位/秒和2个单位/秒的速度相向而行,则几秒后A、B两点相距2个单位长度?
(4)若点A、B以(3)中的速度同时向右运动,点![]() 从原点
从原点![]() 以7个单位/秒的速度向右运动,设运动时间为
以7个单位/秒的速度向右运动,设运动时间为![]() 秒,请问:在运动过程中,
秒,请问:在运动过程中,![]() 的值是否会发生变化?若变化,请用
的值是否会发生变化?若变化,请用![]() 表示这个值;若不变,请求出这个定值.
表示这个值;若不变,请求出这个定值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 在线段
在线段![]() 上,图中共有三条线段
上,图中共有三条线段![]() ,
,![]() 和
和![]() ,若其中有一条线段的长度是另外一条线段长度的2倍,则称点
,若其中有一条线段的长度是另外一条线段长度的2倍,则称点![]() 是线段
是线段![]() 的“巧点”.
的“巧点”.
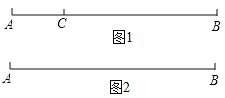
(1)线段的中点_________这条线段的“巧点”;(填“是”或“不是”);
(2)如图2,已知![]() .动点
.动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速运动;点
匀速运动;点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 匀速运动,点
匀速运动,点![]() ,
,![]() 同时出发,当其中一点到达终点时,运动停止.设移动的时间为
同时出发,当其中一点到达终点时,运动停止.设移动的时间为![]() ,当
,当![]() _________
_________![]() 时,
时,![]() 为
为![]() 的“巧点”.
的“巧点”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:“2_3_5_9”,在每个“____”上,填入+,-,×,÷中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若![]() ,请推算“____”上的符号;
,请推算“____”上的符号;
(3)在“2__3__5+9”的“__”上填入符号后,使计算所得数最小,直接写出填上符号后的算式及算式的计算结果的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com