
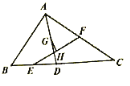
【题目】(1)如图,![]() 是
是![]() 的边
的边![]() 上一点,且
上一点,且![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 分别是
分别是![]() ,
,![]() 的中点,求证:
的中点,求证:![]() .
.
(2)若(1)中的![]() ,其它条件不变,求
,其它条件不变,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1) 连接EG,FG,根据三角形中位线定理可得,EG=![]() AB,FG=
AB,FG=![]() CD,又因为CD=AB,所以EG=FG,又因为H是EF的中点,根据三线合一可得结果;(2)根据中位线定理可得:EG∥AB, FG∥CD,又因为∠ABC=90°,所以∠EGF=90°,即△GEF是等腰直角三角形,所以再根据斜边上的中线等于斜边的一半即可解答.
CD,又因为CD=AB,所以EG=FG,又因为H是EF的中点,根据三线合一可得结果;(2)根据中位线定理可得:EG∥AB, FG∥CD,又因为∠ABC=90°,所以∠EGF=90°,即△GEF是等腰直角三角形,所以再根据斜边上的中线等于斜边的一半即可解答.
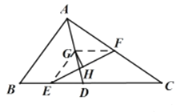
(1)连接EG,FG,
∵E,G分别是BD,AD的中点,
∴EG=![]() AB,
AB,
同理,FG=![]() CD,
CD,
∵CD=AB,
∴EG=FG,
∵H是EF的中点,
∴GH⊥EF
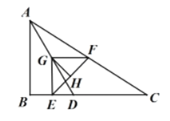
(2)∵E,G分别是BD,AD的中点,
∴EG∥AB,同理FG∥CD,
又∠ABC=90°,
∴∠EGF=90°,
∵H是EF的中点,
∴GH=![]() EF,
EF,
∴![]() =
=![]()


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
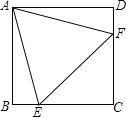
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=![]() .
.
其中正确的序号是 (把你认为正确的都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:

A. A→O→B B. B→A→C C. B→O→C D. C→B→O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点在原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额-生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB的后面有一建筑物CD,在距离CD的正后方30米的观测点P处,以22°的仰角测得建筑物的顶端C恰好挡住教学楼的顶端A,而在建筑物CD上距离地面3米高的E处,测得教学楼的顶端A的仰角为45°,求教学楼AB的高度.(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据《北京晚报》介绍,自2009年故宫博物院年度接待观众首次突破1000万人次之后,每年接待量持续增长,到2018年突破1700万人次,成为世界上接待量最多的博物馆.特别是随着《我在故宫修文物》、《上新了,故宫》等一批电视文博节目的播出,社会上再次掀起故宫热.于是故宫文创营销人员为开发针对不同年龄群体的文创产品,随机调查了部分参观故宫的观众的年龄,整理并绘制了如下统计图表.
2018年参观故宫观众年龄频数分布表
年龄x/岁 | 频数/人数 | 频率 |
20≤x<30 | 80 | b |
30≤x<40 | a | 0.240 |
40≤x<50 | 35 | 0.175 |
50≤x<60 | 37 | c |
合计 | 200 | 1.000 |
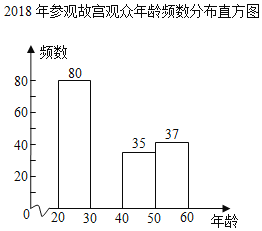
(1)求表中a,b,c的值;
(2)补全频数分布直方图;
(3)从数据上看,年轻观众(20≤x<40)已经成为参观故宫的主要群体.如果今年参观故宫人数达到2000万人次,那么其中年轻观众预计约有 万人次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是菱形
是菱形![]() 边上的一个动点,点
边上的一个动点,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 的方向匀速运动到
的方向匀速运动到![]() 停止,过点
停止,过点![]() 作
作![]() 垂直直线
垂直直线![]() 于点
于点![]() ,已知
,已知![]() ,设点
,设点![]() 走过的路程为
走过的路程为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() (当点
(当点![]() 与点
与点![]() 或点
或点![]() 重合时,
重合时,![]() 的值为
的值为![]() )
)

小腾根据学习函数的经验,对函数随自变量的变化规律进行了探究,下面是小腾的探究过程,请补充完整;
(1)按照下表中自变量的值进行取点,画图,测量,分别得到了以下几组对应值;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,并画出函数的图像;
,并画出函数的图像;

(3)结合函数图像,解决问题,当点![]() 到直线
到直线![]() 的距离恰为点
的距离恰为点![]() 走过的路程的一半时,点P走过的路程约是
走过的路程的一半时,点P走过的路程约是 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
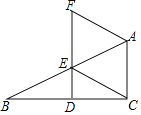
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com