
【题目】某产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点在原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额-生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?

【答案】(1)![]() ,
, ![]() ;(2)W=
;(2)W=![]() ,年产量为75万件时毛利润最大,最大毛利润为1125万元;(3)1080万元
,年产量为75万件时毛利润最大,最大毛利润为1125万元;(3)1080万元
【解析】(1)先设出函数解析式,再通过待定系数法即可得出函数解析式;(2)根据“毛利润=销售额-生产费用”可求出w与x之间的函数关系式,再通过顶点坐标可得出年产量的值及最大的毛利润;(3)由y=360,得出x的值,再通过关于w的二次函数的增减性即可得出答案.
解:(1)![]() ,
, ![]()
(2)W=![]()
=![]()
=![]()
=![]()
∵![]() <0,
<0,
∴当x=75时,W有最大值1125
∴年产量为75万件时毛利润最大,最大毛利润为1125万元
(3)令y=360,得![]() ,解得x=±60(负值舍去)
,解得x=±60(负值舍去)
由图象可知,当0<y≤360时,0<x≤60
由W=![]() 的性质可知,
的性质可知,
当0<x≤60时,W随x的增大而增大
∴当x=60时,W有最大值1080
∴今年最多可获得毛利润1080万元


科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(﹣1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( ) 
A.(0,0)
B.( ![]() ,﹣
,﹣ ![]() )
)
C.(﹣ ![]() ,﹣
,﹣ ![]() )
)
D.(﹣ ![]() ,﹣
,﹣ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面坐标系中△ABO位置如图,已知OA=AB=5,OB=6, 
(1)求A、B两点的坐标.
(2)点Q为y轴上任意一点,直接写出满足:S△ABO=S△AOQ的Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
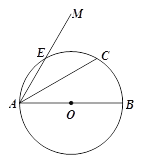
【题目】如图,AB是⊙O的直径,射线AM经过⊙O上的点E,弦AC平分∠MAB,过点C作CD⊥AM,垂足为D.
(1)请用尺规作图将图形补充完整,不写作法,保留痕迹,并证明:CD是⊙O的切线;
(2)若AB=8, ![]() ,求弦AE的长.
,求弦AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 . 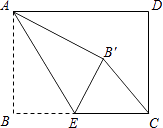
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以OA为斜边作等腰直角△OAB,再以OB为斜边在△OAB外侧作等腰直角△OBC,如此继续,得到8个等腰直角三角形(如图),则图中△OAB与△OHI的面积比值是( ) 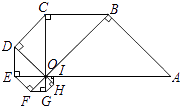
A.32
B.64
C.128
D.256
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com