Question

【题目】如图，AB是⊙O的直径，射线AM经过⊙O上的点E，弦AC平分∠MAB，过点C作CD⊥AM，垂足为D．

（1）请用尺规作图将图形补充完整，不写作法，保留痕迹，并证明：CD是⊙O的切线；

（2）若AB＝8， ，求弦AE的长．

Answer 1

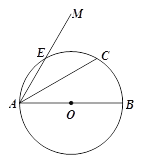
【答案】（1）作图及证明见解析；（2）4

【解析】（1）以C为圆心，大于C到AM的距离为半径作弧分别与AM有两个交点，以这两个交点分别为圆心，以大于这两个交点长的一半为半径作弧，两弧交点一点，过这一点及点D即可得到AM的垂线，连接OC，证∠OCD＝90°即可说明CD是⊙O的切线；（2）作OF⊥AM，得矩形OCDF，可求出OF的值，再通过勾股定理和垂径定理即可求出AE的长.

解：（1）作图正确，痕迹明显

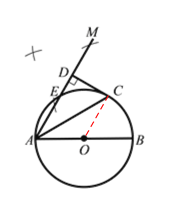
证明：连接OC，则OA＝OC，∴∠OAC＝∠OCA

∵AC平分∠MAB，∴∠OAC＝∠MAC

∴∠OCA＝∠MAC，∴AM∥OC

∵CD⊥AM，垂足为D，∴∠CDM＝90°

∴∠OCD＝∠CDM＝90°，∴OC⊥CD，∴CD是⊙O的切线

（2）作OF⊥AM，垂足为F，

则AF＝EF，四边形OCDF是矩形

∴

在Rt△AOF中，∵

∴

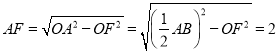
∴AE＝2AF＝4