
【题目】如图,在Rt△ABC中,BC![]() 2,∠BAC
2,∠BAC![]() 30°,斜边AB的两个端点分别在相互垂直的射线OM,ON上滑动,下列结论: ①若C,O两点关于AB对称,则OA
30°,斜边AB的两个端点分别在相互垂直的射线OM,ON上滑动,下列结论: ①若C,O两点关于AB对称,则OA![]() ;②C,O两点距离的最大值为4;③若AB平分CO,则AB⊥CO;④斜边AB的中点D运动路径的长为
;②C,O两点距离的最大值为4;③若AB平分CO,则AB⊥CO;④斜边AB的中点D运动路径的长为![]() .
.
其中正确的是( )
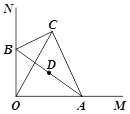
A. ①② B. ①②③ C. ①③④ D. ①②④
【答案】D
【解析】分析:①先根据直角三角形30°的性质和勾股定理分别求AC和AB,由对称的性质可知:AB是OC的垂直平分线,所以![]()
②当OC经过AB的中点E时,OC最大,则C、O两点距离的最大值为4;
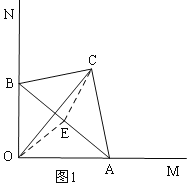
③如图2,当∠ABO=30°时,易证四边形OACB是矩形,此时AB与CO互相平分,但所夹锐角为60°,明显不垂直,或者根据四点共圆可知:A、C、B、O四点共圆,则AB为直径,由垂径定理相关推论:平分弦(不是直径)的直径垂直于这条弦,但当这条弦也是直径时,即OC是直径时,AB与OC互相平分,但AB与OC不一定垂直;
④如图3,半径为2,圆心角为90°,根据弧长公式进行计算即可.
详解:在Rt△ABC中,∵![]()
∴![]()
①若C.O两点关于AB对称,如图1,
∴AB是OC的垂直平分线,
则![]()
所以①正确;
②如图1,取AB的中点为E,连接OE、CE,
∵![]()
∴![]()
当OC经过点E时,OC最大,
则C.O两点距离的最大值为4;
所以②正确;
③如图2,当![]() 时,
时, ![]()
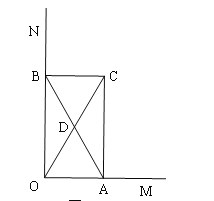
∴四边形AOBC是矩形,
∴AB与OC互相平分,
但AB与OC的夹角为![]() 不垂直,
不垂直,
所以③不正确;
④如图3,斜边AB的中点D运动路径是:以O为圆心,以2为半径的圆周的![]()
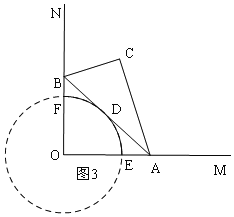
则:![]()
所以④正确;
综上所述,本题正确的有:①②④;
故选D.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】为响应市政府“绿色出行”的号召,小张上班由自驾车改为骑公共自行车.已知小张家距上班地点10千米.他骑公共自行车比自驾车平均每小时少行驶45千米,他从家出发到上班地点,骑公共自行车所用的时间是自驾车所用的时间的4倍.小张骑公共自行车平均每小时行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点在原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额-生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据《北京晚报》介绍,自2009年故宫博物院年度接待观众首次突破1000万人次之后,每年接待量持续增长,到2018年突破1700万人次,成为世界上接待量最多的博物馆.特别是随着《我在故宫修文物》、《上新了,故宫》等一批电视文博节目的播出,社会上再次掀起故宫热.于是故宫文创营销人员为开发针对不同年龄群体的文创产品,随机调查了部分参观故宫的观众的年龄,整理并绘制了如下统计图表.
2018年参观故宫观众年龄频数分布表
年龄x/岁 | 频数/人数 | 频率 |
20≤x<30 | 80 | b |
30≤x<40 | a | 0.240 |
40≤x<50 | 35 | 0.175 |
50≤x<60 | 37 | c |
合计 | 200 | 1.000 |
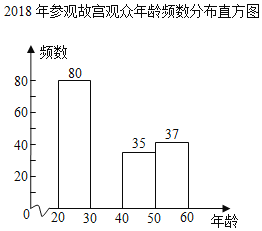
(1)求表中a,b,c的值;
(2)补全频数分布直方图;
(3)从数据上看,年轻观众(20≤x<40)已经成为参观故宫的主要群体.如果今年参观故宫人数达到2000万人次,那么其中年轻观众预计约有 万人次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=-x+4的交点为P(3,m),与y轴交于点A.
(1)求m的值;
(2)如果△PAO的面积为3,求直线y=kx+b的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是菱形
是菱形![]() 边上的一个动点,点
边上的一个动点,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 的方向匀速运动到
的方向匀速运动到![]() 停止,过点
停止,过点![]() 作
作![]() 垂直直线
垂直直线![]() 于点
于点![]() ,已知
,已知![]() ,设点
,设点![]() 走过的路程为
走过的路程为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() (当点
(当点![]() 与点
与点![]() 或点
或点![]() 重合时,
重合时,![]() 的值为
的值为![]() )
)

小腾根据学习函数的经验,对函数随自变量的变化规律进行了探究,下面是小腾的探究过程,请补充完整;
(1)按照下表中自变量的值进行取点,画图,测量,分别得到了以下几组对应值;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,并画出函数的图像;
,并画出函数的图像;

(3)结合函数图像,解决问题,当点![]() 到直线
到直线![]() 的距离恰为点
的距离恰为点![]() 走过的路程的一半时,点P走过的路程约是
走过的路程的一半时,点P走过的路程约是 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(0,3),C(1,0).
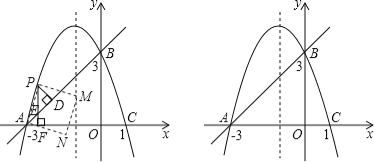
(1)求此抛物线的解析式.
(2)点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.
①动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;
②连接PA,以AP为边作图示一侧的正方形APMN,随着点P的运动,正方形的大小、位置也随之改变.
当顶点M或N恰好落在抛物线对称轴上时,求出对应的P点的坐标.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明每天早上7:30从家出发,到距家![]() 的学校上学,一天,小明以
的学校上学,一天,小明以![]() 的速度上学,
的速度上学,![]() 后小明爸爸发现他发现忘带语文书,爸爸立即带上语文书去追赶小明.
后小明爸爸发现他发现忘带语文书,爸爸立即带上语文书去追赶小明.
(1)如果爸爸以![]() 的速度追小明,爸爸追上小明时距离学校多远?
的速度追小明,爸爸追上小明时距离学校多远?
(2)如果爸爸刚好能在学校门口追上小明,爸爸的速度是多少?
(3)爸爸以![]() 的速度追赶小明,他把书给小明后及时原路原速返回(交书耽误的时间忽略不计),返回家的时间是多少?
的速度追赶小明,他把书给小明后及时原路原速返回(交书耽误的时间忽略不计),返回家的时间是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com