
����Ŀ��С��ÿ������7��30�Ӽҳ����������![]() ��ѧУ��ѧ��һ�죬С����
��ѧУ��ѧ��һ�죬С����![]() ���ٶ���ѧ��
���ٶ���ѧ��![]() ��С���ְַ������������������飬�ְ���������������ȥ��С��.
��С���ְַ������������������飬�ְ���������������ȥ��С��.
��1������ְ���![]() ���ٶ�С�����ְ���С��ʱ����ѧУ��Զ��
���ٶ�С�����ְ���С��ʱ����ѧУ��Զ��
��2������ְָպ�����ѧУ�ſ���С�����ְֵ��ٶ��Ƕ��٣�
��3���ְ���![]() ���ٶ���С�����������С����ʱԭ·ԭ�ٷ��أ����鵢���ʱ����Բ��ƣ������ؼҵ�ʱ���Ƕ��٣�
���ٶ���С�����������С����ʱԭ·ԭ�ٷ��أ����鵢���ʱ����Բ��ƣ������ؼҵ�ʱ���Ƕ��٣�
���𰸡���1���ְ���С��ʱ����ѧУ200�ף���2���ְֵ��ٶ���![]() ����3���ְַ��ؼҵ�ʱ����7��43.
����3���ְַ��ؼҵ�ʱ����7��43.
��������
��1����ְ�t���Ӻ���С�������ݴ�ʱС����ʻ��·��=�ְ���ʻ��·�̣��з��̲��ⷽ�̣�Ȼ������ְ���С��ʱ����ѧУ�ж�Զ��
��2�������С���Ӽҵ�ѧУ��ʱ�䣬Ȼ������ְִӼҵ�ѧУ��ʱ�䣬��������ְֵ��ٶȣ�
��3����ְ�x���Ӻ���С��, ���ݴ�ʱС����ʻ��·��=�ְ���ʻ��·�̣��з��̲��ⷽ�̣����ݰְ�ԭ�ٷ��ؼ����������ʱ��ʱ�䣬�Ӷ�����ְַ��ؼҵ�ʱ��.
�⣺��1����ְ�t���Ӻ���С��
�������֪��80��t��5��=160t
��ã�t=5
��ְ���С��ʱ����ѧУ1000��160��5=200���ף�
�𣺰ְ���С��ʱ����ѧУ200�ף�
��2��С���Ӽҵ�ѧУ����ʱ��Ϊ��1000��80=12.5�����ӣ�
��ְִӼҵ�ѧУ����ʱ��Ϊ��12.5��5=7.5�����ӣ�
��ְֵ��ٶ�Ϊ��1000��7.5=![]()
�𣺰ְֵ��ٶ���![]() ��
��
��3����ְ�x���Ӻ���С��
�������֪��80��x��5��=180x
��ã�x=4
�ְ߰�ԭ�ٷ���
���Ҳ����4����
��ʱ��ʱ��Ϊ��7��30��0:05��0:04��0:04=7��43
�𣺰ְַ��ؼҵ�ʱ����7��43.


 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У�BC![]() 2����BAC
2����BAC![]() 30����б��AB�������˵�ֱ������ֱ������OM��ON�ϻ��������н��ۣ� ����C��O�������AB�Գƣ���OA
30����б��AB�������˵�ֱ������ֱ������OM��ON�ϻ��������н��ۣ� ����C��O�������AB�Գƣ���OA![]() ����C��O�����������ֵΪ4������ABƽ��CO����AB��CO����б��AB���е�D�˶�·���ij�Ϊ
����C��O�����������ֵΪ4������ABƽ��CO����AB��CO����б��AB���е�D�˶�·���ij�Ϊ![]() .
.
������ȷ������ ��
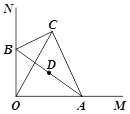
A. �٢� B. �٢ڢ� C. �٢ۢ� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ(![]() )��������ֱ�����dzߵ�ֱ�Ƕ���
)��������ֱ�����dzߵ�ֱ�Ƕ���![]() ������һ��
������һ��
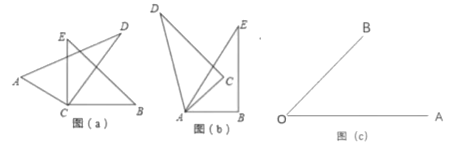
����![]() ����
����![]() __________����
__________����![]() ����
����![]() ___________.
___________.
�ڲ���![]() ��
��![]() �Ķ����к������ϵ����˵������.
�Ķ����к������ϵ����˵������.
(2)��ͼ(![]() )������ͬ�������dz�
)������ͬ�������dz�![]() ��ǵĶ���
��ǵĶ���![]() �غ���һ����
�غ���һ����![]() ��
��![]() �Ķ����кι�ϵ����˵������.
�Ķ����кι�ϵ����˵������.
(3)��ͼ(![]() )����֪
)����֪![]() ����
����![]() (
(![]() ��
��![]() ���������
���������![]() )����
)����![]() ��
��![]() ���ڲ�����ֱ��д��
���ڲ�����ֱ��д��![]() ��
��![]() �Ķ�����ϵ.
�Ķ�����ϵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���������ij�ֹ�Ʊ1000�ɣ�ÿ��27Ԫ��

��1������������ʱ��ÿ���Ƕ���Ԫ��
��2�������������ÿ�ɶ���Ԫ����ͼ���ÿ�ɶ���Ԫ��
��3����С���ڱ���������̼۽���Ʊȫ������������Ϊ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���и���д������ŵ���Ϸ����2_3_5_9������ÿ����____���ϣ�����+��-���������е�ijһ�������ظ�ʹ�ã���Ȼ�������.
��1�����㣺![]() ��
��
��2����![]() ����������____���ϵķ��ţ�
����������____���ϵķ��ţ�
��3������2__3__5+9������__����������ź�ʹ������������С��ֱ��д�����Ϸ��ź����ʽ����ʽ�ļ���������Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ��![]() ������ͬһֱ���ϣ�
������ͬһֱ���ϣ�![]() .
.
��1����֪��![]() ��ֱ��
��ֱ��![]() �ϣ������������벹������ͼ�Σ�����
�ϣ������������벹������ͼ�Σ�����![]() �ij���
�ij���
![]()
��2����֪��![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬�����������벹������ͼ�Σ�����
���е㣬�����������벹������ͼ�Σ�����![]() �ij���ֱ��д��
�ij���ֱ��д��![]() ��
��![]() �ij����ڵ�������ϵ��
�ij����ڵ�������ϵ��
![]()
��3����֪��![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬�����������벹������ͼ�Σ�����
���е㣬�����������벹������ͼ�Σ�����![]() �ij���ֱ��д��
�ij���ֱ��д��![]() ��
��![]() �ij����ڵ�������ϵ.
�ij����ڵ�������ϵ.
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=![]() Ϊ������������
������������
��1����k��ֵ��
��2������ͼ���ڵ��� �������ڣ��ڸ������ڣ�y��x������� ��������仯�����
��3�������2��x����![]() ʱ��y��ȡֵ��Χ��
ʱ��y��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAD������BEC��ƽ�����Ƶ�B��ת60�����ã���AB��BC��BE��CE������DE.
��1����֤����BDE�ա�BCE��
��2�����ж��ı���ABED����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�о���ѧϰС����̽�����ε���ֽ����ʱ����һ��ֱ�����ǰ��ֱ�Ƕ����ƾ���ABCD��AB��BC���ĶԽ��ߵĽ���O��ת���١��ڡ�������ͼ�е�M��N�ֱ�Ϊֱ�������ε�ֱ�DZ������ABCD�ı�CD��BC�Ľ��㡣
����ѧϰС���Ա����ķ���ͼ�������ǰ�һֱ�DZ���OD�غϣ��У�BN2=CD2+CN2����ͼ���У����ǰ�һ����OC�غϣ���CN2=BN2+CD2�������������Ա��ͼ����ͼ���з��ֵĽ���ѡ����һ˵�����ɡ�

����̽��ͼ����BN��CN��CM��DN�������߶�֮���������ϵ��д����Ľ��ۣ���˵�����ɡ�

��������ABCD��Ϊ�߳�Ϊ1��������ABCD��ֱ�����ǰ��ֱ�Ƕ�����O����ת��ͼ������ֱ�DZ���AB��BC�ֱ���M��N��ֱ��д��BN��CN��CM��DM�������߶�֮ ���������������ϵ������Ҫ֤����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com