
【题目】如图,在数轴上,点![]() 为原点,点
为原点,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,且
,且![]() 满足
满足![]()
(1)A、B两点对应的数分别为![]() _____,
_____,![]() ______;
______;
(2)若将数轴折叠,使得![]() 点与
点与![]() 点重合,则原点
点重合,则原点![]() 与数______表示的点重合.
与数______表示的点重合.
(3)若点A、B分别以4个单位/秒和2个单位/秒的速度相向而行,则几秒后A、B两点相距2个单位长度?
(4)若点A、B以(3)中的速度同时向右运动,点![]() 从原点
从原点![]() 以7个单位/秒的速度向右运动,设运动时间为
以7个单位/秒的速度向右运动,设运动时间为![]() 秒,请问:在运动过程中,
秒,请问:在运动过程中,![]() 的值是否会发生变化?若变化,请用
的值是否会发生变化?若变化,请用![]() 表示这个值;若不变,请求出这个定值.
表示这个值;若不变,请求出这个定值.
![]()
【答案】(1)-8;6;(2)-2;(3)1.5秒或2秒后A、B两点相距2个单位长度;(4)不会发生变化,定值为20.
【解析】
根据绝对值及平方的非负数性质即可求出a、b的值;(2)根据a、b的值可得AB对折点表示的数,根据两点间的距离即可得答案;(3)分两种情况:①相遇前相距2个单位长度;②相遇后相距2个单位长度;利用距离=时间×速度即可得答案;(4)根据两点间距离公式,利用距离=时间×速度用t分别表示出AP、OB、OP的长,计算![]() 的值即可得答案.
的值即可得答案.
(1)∵![]() ,
,
∴a+8=0,b-6=0,
解得:a=-8,b=6,
故答案为:-8,6
(2)∵a=-8,b=6,将数轴折叠,使得A点与B点重合,
∴对折点表示的数是[6+(-8)]÷2=-1,
∵-1与原点的距离是1,
∴原点关于-1的对称点表示的数是-2,即原点O与数-2表示的点重合,
故答案为:-2
(3)①相遇前相距2个单位长度:
t=[6-(-8)-2]÷(4+2)=1.5(秒)
②相遇后相距2个单位长度:
t=[6-(-8)+2]÷(4+2)=2(秒)
综上所述:1.5秒或2秒后A、B两点相距2个单位长度.
(4)AP+2OB-OP的值不会发生变化.
∵OP=7t,OA=-8+4t,
∴AP=7t-(-8+4t)=3t+8,
∵OB=6+2t,
∴AP+2OB-OP=3t+8+2(6+2t)-7t=3t+8+12+4t-7t=20,
∴AP+2OB-OP的值不会发生变化,定值为20.


科目:初中数学 来源: 题型:
【题目】河西中学九年级共有9个班,300名学生,学校要对该年级学生数学学科学业水平测试成绩进行抽样分析,请按要求回答下列问题:
收集数据
(1)若从所有成绩中抽取一个容量为36的样本,以下抽样方法中最合理的是 .
①在九年级学生中随机抽取36名学生的成绩;
②按男、女各随机抽取18名学生的成绩;
③按班级在每个班各随机抽取4名学生的成绩.
整理数据
(2)将抽取的36名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图如下.请根据图表中数据填空:
①C类和D类部分的圆心角度数分别为 °、 °;
②估计九年级A、B类学生一共有 名.

成绩(单位:分) | 频数 | 频率 |
A类(80~100) | 18 |
|
B类(60~79) | 9 |
|
C类(40~59) | 6 |
|
D类(0~39) | 3 |
|
分析数据
(3)教育主管部门为了解学校教学情况,将河西、复兴两所中学的抽样数据进行对比,得下表:
学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
河西中学 | 71 | 52 | 432 | 0.75 |
复兴中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校本次测试成绩较好,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB的后面有一建筑物CD,在距离CD的正后方30米的观测点P处,以22°的仰角测得建筑物的顶端C恰好挡住教学楼的顶端A,而在建筑物CD上距离地面3米高的E处,测得教学楼的顶端A的仰角为45°,求教学楼AB的高度.(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:

(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是菱形
是菱形![]() 边上的一个动点,点
边上的一个动点,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 的方向匀速运动到
的方向匀速运动到![]() 停止,过点
停止,过点![]() 作
作![]() 垂直直线
垂直直线![]() 于点
于点![]() ,已知
,已知![]() ,设点
,设点![]() 走过的路程为
走过的路程为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() (当点
(当点![]() 与点
与点![]() 或点
或点![]() 重合时,
重合时,![]() 的值为
的值为![]() )
)

小腾根据学习函数的经验,对函数随自变量的变化规律进行了探究,下面是小腾的探究过程,请补充完整;
(1)按照下表中自变量的值进行取点,画图,测量,分别得到了以下几组对应值;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,并画出函数的图像;
,并画出函数的图像;

(3)结合函数图像,解决问题,当点![]() 到直线
到直线![]() 的距离恰为点
的距离恰为点![]() 走过的路程的一半时,点P走过的路程约是
走过的路程的一半时,点P走过的路程约是 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
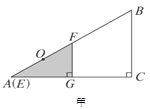
【题目】如图甲,有两个形状完全相同的直角三角形ABC和EFG叠放在一起(点A与点E重合),已知AC![]() 8 cm,BC
8 cm,BC![]() 6 cm,∠C
6 cm,∠C![]() 90°,EG
90°,EG![]() 4 cm,∠EGF
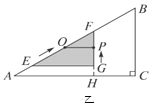
4 cm,∠EGF![]() 90°,O是△EFG斜边上的中点. 如图乙,若整个△EFG从图甲的位置出发,以1 cm/s的速度沿射线AB方向平移,在△EFG平移的同时,点P从△EFG的顶点G出发,以1 cm/s的速度在直角边GF上向点F运动,当点P到达点F时,点P停止运动,△EFG也随之停止平移. 设运动时间为x(s),FG的延长线交AC于H,四边形OAHP的面积为y(cm2)(提示:不考虑点P与G、F重合的情况).
90°,O是△EFG斜边上的中点. 如图乙,若整个△EFG从图甲的位置出发,以1 cm/s的速度沿射线AB方向平移,在△EFG平移的同时,点P从△EFG的顶点G出发,以1 cm/s的速度在直角边GF上向点F运动,当点P到达点F时,点P停止运动,△EFG也随之停止平移. 设运动时间为x(s),FG的延长线交AC于H,四边形OAHP的面积为y(cm2)(提示:不考虑点P与G、F重合的情况).
(1)当x为何值时,OP∥AC?
(2)求y与x之间的函数关系式,并确定自变量x的取值范围;
(3)是否存在某一时刻,使四边形OAHP面积与△ABC面积的比为![]() ?若存在,求出x的值;若不存在,说明理由.
?若存在,求出x的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
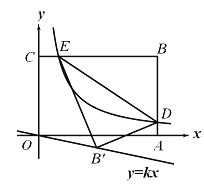
【题目】如图,平面直角坐标系![]() 中,矩形
中,矩形![]() 的边
的边![]() 、
、![]() 分别落在
分别落在![]() 、
、![]() 轴上,点
轴上,点![]() 坐标为
坐标为![]() ,反比例函数
,反比例函数![]() 的图象与
的图象与![]() 边交于点
边交于点![]() ,与
,与![]() 边交于点
边交于点![]() ,连结
,连结![]() ,将
,将![]() 沿
沿![]() 翻折至
翻折至![]() 处,点
处,点![]() 恰好落在正比例函数
恰好落在正比例函数![]() 图象上,则
图象上,则![]() 的值是
的值是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情況记录如下(单位:![]() ):
):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .(假定开始计时时,守门员正好在球门线上)
.(假定开始计时时,守门员正好在球门线上)
(1)守门员最后是否回到球门线上?
(2)守门员在这段时间内共跑了多少米?
(3)如果守门员离开球门线的距离超过10米(不包括10米),则对方球员挑射极可能造成破门.请问在这一时间段内,对方球员有几次挑射破门的机会?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com