
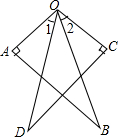
 如图,OA⊥AB,OC⊥CD,OA=OC,OB=OD,求证:∠1=∠2.
如图,OA⊥AB,OC⊥CD,OA=OC,OB=OD,求证:∠1=∠2.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
| 距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
| 温度(℃) | 20 | 14 | 8 | 2 | -4 | -10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
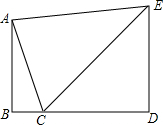 如图,小明想利用自己所学的数学知识测量连接塔AB的尖端和地面间的一条空中速滑索道AC的长度,小明先测得塔尖A在点C的北偏西22°方向,然后沿坡比为1:1(即tan∠ECD=1)的斜坡以18/分的速度步行2分钟到达E,测得点A的俯角为8°,若点A、B、C、D、E,都在同一平面内,且B、C、D三点共线.
如图,小明想利用自己所学的数学知识测量连接塔AB的尖端和地面间的一条空中速滑索道AC的长度,小明先测得塔尖A在点C的北偏西22°方向,然后沿坡比为1:1(即tan∠ECD=1)的斜坡以18/分的速度步行2分钟到达E,测得点A的俯角为8°,若点A、B、C、D、E,都在同一平面内,且B、C、D三点共线. 查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不等边三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
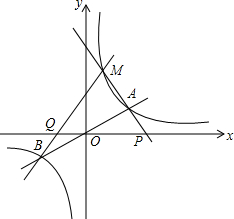 如图,已知双曲线y=$\frac{{k}_{1}+3}{x}$(k1为常数)与直线y=k2x(k2为常数)相交于A,B两点,双曲线在第一象限内部分有一点M(点M在A的左侧)在双曲线y=$\frac{{k}_{1}+3}{x}$上,设直线MA,MB分别与x轴分别交于P,Q两点.若MA=m•AP,MB=n•QB,则n-m的值是2.
如图,已知双曲线y=$\frac{{k}_{1}+3}{x}$(k1为常数)与直线y=k2x(k2为常数)相交于A,B两点,双曲线在第一象限内部分有一点M(点M在A的左侧)在双曲线y=$\frac{{k}_{1}+3}{x}$上,设直线MA,MB分别与x轴分别交于P,Q两点.若MA=m•AP,MB=n•QB,则n-m的值是2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
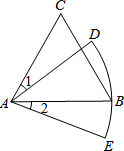 如图,△ABC是等边三角形,AC=6,以点A为圆心,AB长为半径画弧DE,若∠1=∠2,则弧DE的长为( )
如图,△ABC是等边三角形,AC=6,以点A为圆心,AB长为半径画弧DE,若∠1=∠2,则弧DE的长为( )| A. | 1π | B. | 1.5π | C. | 2π | D. | 3π |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com