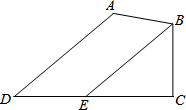
已知:如图.在四边形ABCD中.∠A=130°.∠C=90°.∠D=40°.BE∥AD交CD于点E．求证:BE平分∠ABC．题目和参考答案——青夏教育精英家教网—

14．

已知：如图，在四边形ABCD中，∠A=130°，∠C=90°，∠D=40°，BE∥AD交CD于点E．求证：BE平分∠ABC．

分析先根据四边形内角和定理求出∠ABC的度数，再由平行线的性质求出∠ABE的度数，进而可得出结论．

解答证明：∵在四边形ABCD中，∠A=130°，∠C=90°，∠D=40°，
∴∠ABC=360°-130°-90°-40°=100°．
∵BE∥AD，
∴∠ABE=180°-∠A=180°-130°=50°，
∴∠ABE=$\frac{1}{2}$∠ABC，即BE平分∠ABC．

点评本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．

练习册系列答案

小学同步学考优化设计小超人作业本系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

4．

如图，河堤横断面迎水坡AB的坡比是1：$\sqrt{3}$，堤高BC=10m，求坡面AB的长．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

5．

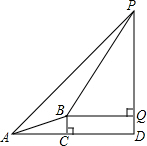如图，某校综合实践活动小组同学欲测量台阶平台上电线杆PQ的高度，他们在台阶下A点处测得电线杆顶端P的仰角∠PAC为45°，沿着台阶走到台阶上的点B处，测得电线杆顶端P的仰角∠PBQ为57°，已知BC的高度为2m，台阶AB的坡比为1：3，BQ∥AC，求电线杆PQ的高度．（参考数据：tan57°≈$\frac{3}{2}$，sin57°≈$\frac{4}{5}$）

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

2．

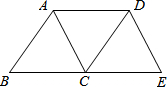如图，将△ABC沿BC方向平移得到△DCE，连结AD，下列条件中能够判定四边形ACED为菱形的是（　　）

A．

∠ACB=60°

B．

∠B=60°

C．

AB=BC

D．

AC=BC

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

9．对某条路线的长度进行5次测量，得到5个结果（单位：km）：x₁=104，x₂=101，x₃=102，x₄=104，x₅=103．如果用x作为这条路线长度的近似值，要使得（x-x₁）²+（x-x₂）²+…+（x-x₅）²的值最小，x应选取这5次测量结果的（　　）

A．

中位数

B．

众数

C．

平均数

D．

最小值

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

19．一个不透明的袋子里装有红、黄、蓝三种颜色的小球（除颜色外其余都相同），其中红球2个（分别标有1号、2号）蓝球1个，黄球1个．从口袋中任意摸出一个球，记下颜色后放回，再从口袋中随机摸出一个．
（1）请用画树状图或列表法，列出所有可能的情况；
（2）求两次摸到不同颜色球的概率．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

4．

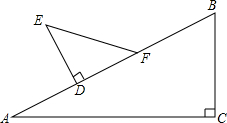如图△ABC中，∠C=90°，∠A=30°，BC=5cm；△DEF中∠D=90°，∠E=45°，DE=3cm．现将△DEF的直角边DF与△ABC的斜边AB重合在一起，并将△DEF沿AB方向移动（如图）．在移动过程中，D、F两点始终在AB边上（移动开始时点D与点A重合，一直移动至点F与点B重合为止）．
（1）当△DEF移动至什么位置，即AD的长为多少时，E、B的连线与AC平行？
（2）在△DEF的移动过程中，是否存在某个位置，使得∠EBD=22.5°？如果存在，求出AD的长度；如果
不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

1．