
| A. | 中位数 | B. | 众数 | C. | 平均数 | D. | 最小值 |
分析 先设出y=(x-x1)2+(x-x2)2+(x-x3)2+…+(x-x5)2,然后进行整理得出y=5x2-2(x1+x2+x3+…+x5)x+(x12+x22+x32+…+x52),再求出二次函数的最小值即可得出答案.
解答 解:设y=(x-x1)2+(x-x2)2+(x-x3)2+…+(x-x5)2=x2-2xx1+x12+x2-2xx2+x22+x2-2xx3+x32+…+x2-2xx5+x52=5x2-2(x1+x2+x3+…+x5)x+(x12+x22+x32+…+x52),
则当x=-$\frac{-2({x}_{1}+{x}_{2}+{x}_{3}+{x}_{4}+{x}_{5})}{2×5}$=$\frac{{x}_{1}+{x}_{2}+{x}_{3}+{x}_{4}+{x}_{5}}{5}$时,时,二次函数y=nx2-2(x1+x2+x3+…+xn)x+(x12+x22+x32+…+xn2)最小,
则x应选取这5次测量结果的平均数;
故选C.
点评 此题考查了方差,关键是设y=(x-x1)2+(x-x2)2+(x-x3)2+…+(x-xn)2,得到一个二次函数,用到的知识点是求二次函数的最小值.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
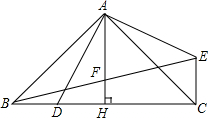 已知:AC=AB,AD=AE,AD⊥AE,AB⊥AC,垂足均为点A,连接BE,AH⊥BC,垂足为点H,AH与BE相交于F.求证:BF=EF.
已知:AC=AB,AD=AE,AD⊥AE,AB⊥AC,垂足均为点A,连接BE,AH⊥BC,垂足为点H,AH与BE相交于F.求证:BF=EF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
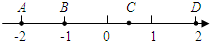 如图,数轴上用点A,B,C,D表示有理数,下列语句正确的有( )
如图,数轴上用点A,B,C,D表示有理数,下列语句正确的有( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
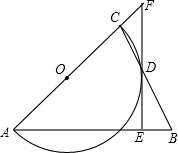 如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.
如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
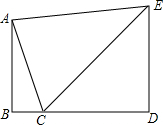 如图,小明想利用自己所学的数学知识测量连接塔AB的尖端和地面间的一条空中速滑索道AC的长度,小明先测得塔尖A在点C的北偏西22°方向,然后沿坡比为1:1(即tan∠ECD=1)的斜坡以18/分的速度步行2分钟到达E,测得点A的俯角为8°,若点A、B、C、D、E,都在同一平面内,且B、C、D三点共线.
如图,小明想利用自己所学的数学知识测量连接塔AB的尖端和地面间的一条空中速滑索道AC的长度,小明先测得塔尖A在点C的北偏西22°方向,然后沿坡比为1:1(即tan∠ECD=1)的斜坡以18/分的速度步行2分钟到达E,测得点A的俯角为8°,若点A、B、C、D、E,都在同一平面内,且B、C、D三点共线. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com