
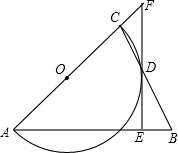
 如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.
如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.分析 (1)首先连接OD,AD,根据AC是直径,判断出AD⊥BC,进而判断出D是BC的中点;然后判断出OD∥AB,再根据DE⊥AB,判断出DE⊥OD,进而判断出DE是⊙O的切线即可.
(2)根据OD∥AB,可得$\frac{FO}{FA}=\frac{OD}{AE}$,据此求出CF的值是多少即可.
解答 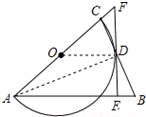 (1)证明:连接OD,AD,
(1)证明:连接OD,AD,
∵AC是直径,
∴∠ADC=90°,
即AD⊥BC,
∵AC=AB,
∴CD=BD,
∵AO=OC,
∴OD∥AB,
∵DE⊥AB,
∴DE⊥OD,
∵OD是半径,
∴DE是⊙O的切线.
(2)解:∵OD∥AB,
∴$\frac{FO}{FA}=\frac{OD}{AE}$,
∵FO=CF+3,FA=CF+3×2=CF+6,AE=AB-BE=AC-BE=3×2-1=5,
∴$\frac{CF+3}{CF+6}=\frac{3}{5}$
解得CF=1.5,
即CF的值是1.5.
点评 (1)此题主要考查了切线的判定,要熟练掌握,解答此题的关键是要明确切线必须满足两个条件:a、经过半径的外端;b、垂直于这条半径,否则就不是圆的切线.
(2)此题还考查了平行线的性质和应用,以及等腰三角形的性质和应用,要熟练掌握.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:选择题
| A. | 8×1011元 | B. | 80×1010元 | C. | 8000×108元 | D. | 8×103元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 中位数 | B. | 众数 | C. | 平均数 | D. | 最小值 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
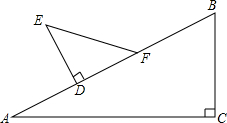 如图△ABC中,∠C=90°,∠A=30°,BC=5cm;△DEF中∠D=90°,∠E=45°,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动(如图).在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动至点F与点B重合为止).
如图△ABC中,∠C=90°,∠A=30°,BC=5cm;△DEF中∠D=90°,∠E=45°,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动(如图).在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动至点F与点B重合为止).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{7}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
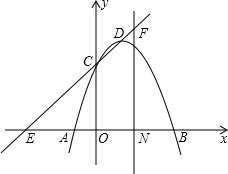 已知抛物线经过A(-1,)、B(3,0),C(0,3),点D为抛物线的顶点.
已知抛物线经过A(-1,)、B(3,0),C(0,3),点D为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 尼泊尔地震牵动着全中国人民的心,中国红十字基金会开展了“一方有难,八方支援”的赈灾活动.5月15日,中国红十字基金会联手北京成龙慈善基金会等共同出资400万元人民币,采购5000只“赈济家庭箱”(“赈济家庭箱”包括当地受灾群众急需的毛毯、防潮垫、睡袋、雨衣、服装、餐具、个人护理用品等),作为首批物资援助尼泊尔地震灾区.该基金会计划到第三批援助物资为止共采购18200只“赈济家庭箱”.
尼泊尔地震牵动着全中国人民的心,中国红十字基金会开展了“一方有难,八方支援”的赈灾活动.5月15日,中国红十字基金会联手北京成龙慈善基金会等共同出资400万元人民币,采购5000只“赈济家庭箱”(“赈济家庭箱”包括当地受灾群众急需的毛毯、防潮垫、睡袋、雨衣、服装、餐具、个人护理用品等),作为首批物资援助尼泊尔地震灾区.该基金会计划到第三批援助物资为止共采购18200只“赈济家庭箱”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com