
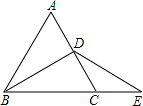
 如图,点C在BE上,BD是等边△ABC的中线,CE=CD,求证:DE=DB.
如图,点C在BE上,BD是等边△ABC的中线,CE=CD,求证:DE=DB. 分析 根据等边三角形的性质得到∠ABC=∠ACB=60°,∠DBC=30°,再根据角之间的关系求得∠DBC=∠CED,根据等角对等边即可得到DB=DE.
解答 证明:∵△ABC是等边三角形,BD是中线,
∴∠ABC=∠ACB=60°.
∠DBC=30°(等腰三角形三线合一).
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=$\frac{1}{2}$∠BCD=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边).
点评 此题主要考查学生对等边三角形的性质及三角形外角的性质的理解及运用;利用三角形外角的性质得到∠CDE=30°是正确解答本题的关键.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,将矩形ABCD绕点B按顺时针方向旋转一个角α(0°<α<180°),得矩形BEFG,直线BG,EF交直线CD于点P,H.找出与BP相等的线段,并给出证明.
已知:如图,将矩形ABCD绕点B按顺时针方向旋转一个角α(0°<α<180°),得矩形BEFG,直线BG,EF交直线CD于点P,H.找出与BP相等的线段,并给出证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,两个大小不同正方形并排放在一起,已知大正方形的边长是4,以点B为圆心.边AB长为半径画圆弧,联结AF、CF,求阴影部分的面积.(结果保留π).
如图,两个大小不同正方形并排放在一起,已知大正方形的边长是4,以点B为圆心.边AB长为半径画圆弧,联结AF、CF,求阴影部分的面积.(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com