
 已知:如图,将矩形ABCD绕点B按顺时针方向旋转一个角α(0°<α<180°),得矩形BEFG,直线BG,EF交直线CD于点P,H.找出与BP相等的线段,并给出证明.
已知:如图,将矩形ABCD绕点B按顺时针方向旋转一个角α(0°<α<180°),得矩形BEFG,直线BG,EF交直线CD于点P,H.找出与BP相等的线段,并给出证明. 分析 BP=PH,由矩形的对边平行可得∠ABP=∠BPH=α、∠CHE=180°-α,根据旋转性质知∠CBE=α,BC=BE,证Rt△BCH≌Rt△BEH可得∠PHB=∠BHE=$\frac{1}{2}$∠CHE=90°-$\frac{1}{2}$α,∠HBE=∠HBC=$\frac{1}{2}$∠CBE=$\frac{1}{2}$α,结合∠PBH=∠PBE-∠HBE=90°-$\frac{1}{2}$α得∠PHB=∠PBH,从而得出BP=PH.
解答 解:BP=PH,
如图,连接PH,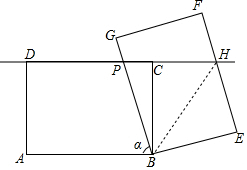
∵四边形ABCD和四边形BEFG是矩形,
∴∠BCH=∠E=90°,AB∥CD、BG∥EF,
∴∠ABP=∠BPH=α,∠CHE=180°-α,
由旋转性质可得∠CBE=α,BC=BE,
在Rt△BCH和Rt△BEH中,
∵BC=BE,BH=BH,
∴Rt△BCH≌Rt△BEH,
∴∠PHB=∠BHE=$\frac{1}{2}$∠CHE=90°-$\frac{1}{2}$α,∠HBE=∠HBC=$\frac{1}{2}$∠CBE=$\frac{1}{2}$α,
∴∠PBH=∠PBE-∠HBE=90°-$\frac{1}{2}$α,
∴∠PHB=∠PBH,
∴BP=PH.
点评 本题主要考查旋转的性质、矩形的性质、全等三角形的判定与性质等知识点,熟练掌握旋转的性质:①对应点到旋转中心的距离相等.②对应点与旋转中心所连线段的夹角等于旋转角. ③旋转前、后的图形全等是解题的关键.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
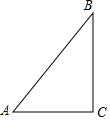 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,r为半径画⊙C,请根据下列条件,求半径r的值或取值范围.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,r为半径画⊙C,请根据下列条件,求半径r的值或取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,CD为中线,tanB=$\frac{1}{2}$,sinA=$\frac{3}{5}$,CA=10,求cos∠ADC的值.
如图,在△ABC中,CD为中线,tanB=$\frac{1}{2}$,sinA=$\frac{3}{5}$,CA=10,求cos∠ADC的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:在矩形ABCD中,AB=6m,BC=8m,动点P以2m/s的速度从A点出发,沿AC向C点移动,同时动点Q以1m/s的速度从点C出发,沿CB向点B移动,设P、Q两点移动的时间为t秒(0<t<5).
如图:在矩形ABCD中,AB=6m,BC=8m,动点P以2m/s的速度从A点出发,沿AC向C点移动,同时动点Q以1m/s的速度从点C出发,沿CB向点B移动,设P、Q两点移动的时间为t秒(0<t<5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,∠B=30°,O为AB上一点,AO=k,⊙O的半径为1.问k为何值时,⊙O与AC:
如图,在△ABC中,∠C=90°,∠B=30°,O为AB上一点,AO=k,⊙O的半径为1.问k为何值时,⊙O与AC:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com